Matrix Multiplication Linear System
From here the solution represented by the column matrix x x x can be obtained by left multiplying both sides of the equation by the inverse of the coefficient matrix A 1 A-1 A 1. 2x 1 3x 2 - x 3.
Matrix Algebra
Thus we want to solve a system AXB.
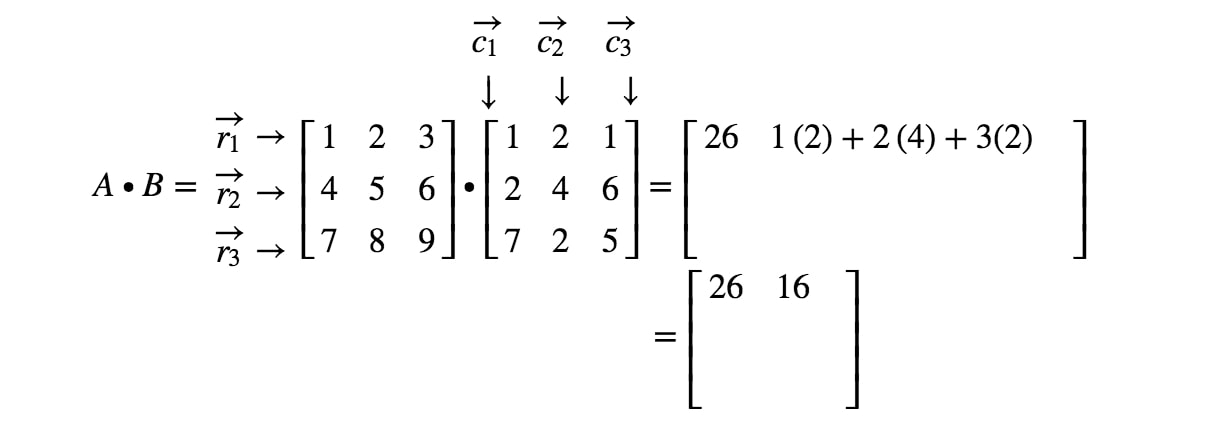
Matrix multiplication linear system. Matrix multiplication rank solving linear systems 1 Matrix Vector Multiplication Ax 2 When is Ax b Solvable. Of the matrix product AB is a linear combination of the rows of B with coecients taken from the jth row of A. A11 x1 a12 x2 a13 x3 a14 x4 b1.
A x b. Adxbdycd -adx-aey-af Add to get. Observe that each component of the product vector corresponds to one of the equations in the system.
Any linear system of n equations in n variables can be solved by this method. These systems may consist of 3 4 equations or may be comprised of hundreds of equations. Usually this will be a row vector multiplied with a column vector of the same size.
Say we are given a system of n linear equations and n unknowns. For the dot product we multiply each pair of entries from the first and the second vector and we sum these products. Theorem SLEMM Systems of Linear Equations as Matrix Multiplication The set of solutions to the linear system LSAb L S A b equals the set of solutions for x x in the vector equation Axb A x b.
3 Reduced Row Echelon Form and Rank 4 Matrix Multiplication 5 Key Connection to Di erential Equations 1Matrix Vector Multiplication Ax Example 1. Now we can define the linear transformation. For any matrix Awith dimension at most n Op n.
A Linear System as a Matrix Equation Consider the linear system Lets construct the coefficient matrix and multiply it by on the right. We have all seen some linear systems in arithmetic high school algebra and pre calculus courses. You do this with each number in the row and coloumn then move to the next row and coloumn and do the same.
Bdy-aey cd-af bd-aey cd-af. While there has been remarkable progress for the special cases of graph structured linear systems in the general setting the bit complexity of solving an n times n linear system Axb is tildeOnomega where omega 2372864 is the matrix multiplication exponent. First we define the so-called dot product or inner product of two vectors.
We multiply rows by coloumns. As seen before a system of equations can be represented by the matrix multiplication A x b. A four by four system looks like this.
X 1 - x 2 3x 3. This means you take the first number in the first row of the second matrix and scale multiply it with the first coloumn in the first matrix. It still features in the work but in a complementary role.
Let us now define matrix multiplication. Here we use the Or pq notation to hide lower-order terms speci cally Or p fp nqq denotes Op fp nq logcp fp nqqq for some absolute constant c. 1 q non-zeros and condition number nOp 1q a linear system in Acan be solved to accuracy.
Mutiply the first equation by d and the second by -a to get. A31 x1 a32 x2 a33 x3 a34 x4 b3. Matrices can be used to describe a linear system of equations as well as solve them using matrix multiplication.
A21 x1 a22 x2 a23 x3 a24 x4 b2. Matrix multiplication for moderately sparse instances. The new proof finds a quicker way of solving a large class of linear systems by sidestepping one of the main techniques typically used in the process.
That technique called matrix multiplication previously set a hard speed limit on just how quickly linear systems could be solved. 132 Systems of linear equations Motivated by Viewpoint 3 concerning matrix multiplicationin particular that Ax x 1A 1 x2A2 xnAn where A 1An are the columns of a matrix A and x x 1xn 2 Rnwe make the following definition. A x b A 1 A x A 1 b x A 1 b.
Using matrix multiplication we may define a system of equations with the same number of equations as variables as AXB To solve a system of linear equations using an inverse matrix let A be the coefficient matrix let X be the variable matrix and let B be the constant matrix.
4 Multiplication Of Matrices
Matrix Algebra
Solving Linear Systems Using Matrices Youtube
Visualizing Matrix Multiplication As A Linear Combination Dzone Big Data
Matrices Systems Of Linear Equations Ppt Download
Part 5 Row Picture And Column Picture By Avnish Linear Algebra Medium
A Complete Beginners Guide To Matrix Multiplication For Data Science With Python Numpy By Chris The Data Guy Towards Data Science
Linear Algebra Britannica
Ex 2 Solve A System Of Two Equations Using A Matrix Equation Youtube
How To Multiply Two Matrices Together Studypug
Matrix Multiplication Calculator
Multiplying Matrices Article Matrices Khan Academy
Dot Product In Linear Algebra For Data Science Using Python By Harshit Tyagi Towards Data Science
How To Solve A System Of Equations On The Ti 84 Plus Dummies
Properties Of Matrix Multiplication Article Khan Academy
Matrix Algebra
Multiplying Matrices Video Khan Academy
5 4 A Matrix Formulation Of The Multiple Regression Model Stat 462
Introduction To Matrices And Vectors Multiplication Using Python Numpy
