Matrix Vector Multiplication Pseudocode
Suppose we have an n n matrix M whose element in row i and column j will be denoted mij. If It Is Not Possible.
Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
The operations involving loops and calculations in this program are similar to those in the previous one.
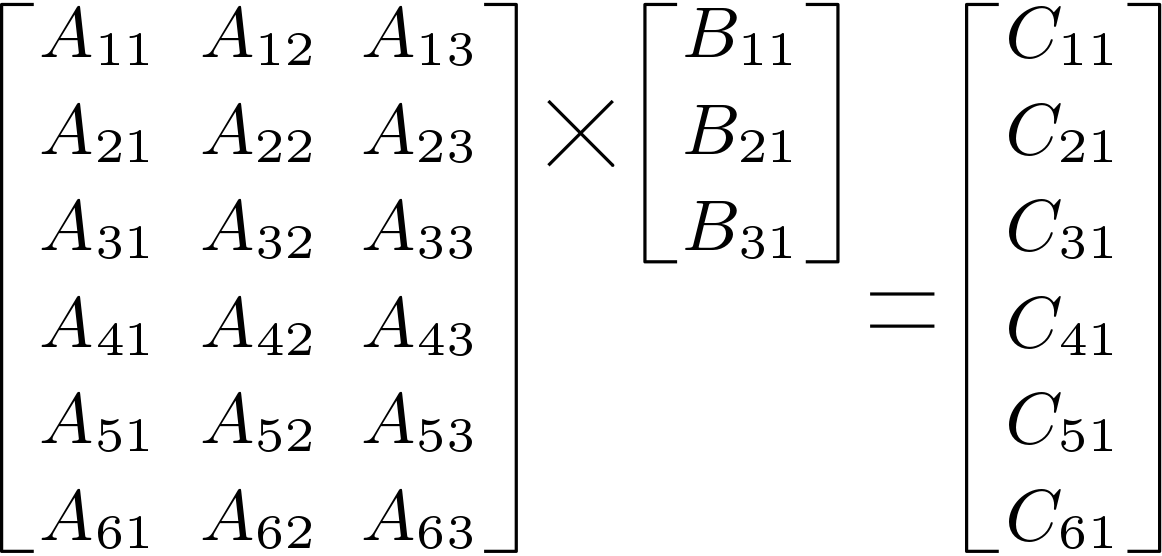
Matrix vector multiplication pseudocode. The final step in the MapReduce algorithm is to produce the matrix A B. Matrix-matrix multiplication takes a triply nested loop. Sparse Matrix-Vector Multiplication SpMV is a Level-2 BLAS operation between a sparse matrix and a dense vector y A x y described element-wise by Equation 1.
ConsoleWriteLinetodoublepenetration the elements of Matrix. 813 Matrix Multiplication for Banded Matrices. Matrix-vector multiplication is the sequence of inner product computations.
Each cell of the matrix is labelled as Aij and Bij. Write Pseudocode That Will Allow You To Do Matrix-Vector Multiplication. The inner product of the One row vector from matrix A.
Element 3 in matrix A is called A21 ie. Returns The Dot Product Of The Two Arrays If Possible. A e b g a f b h c e d g c f d h.
Consider the following matrices A and B. Mapper for Matrix A k vi k A j Aij for all k Mapper for Matrix B k vi k B j Bjk for all i. Now One step matrix multiplication has 1 mapper and 1 reducer.
Array Of Numbers V2 array Of Numbers Outputs. Public void ReadMatrix ConsoleWriteLinen Size of Matrix 1. Then the matrix-vector product is the vector x of length n whose ith element xi is given by x i j 1 n m i j.
This architec-ture is described in detail in our proposal dated August 13 1982. The unit of. The reduce function will compute.
The reduce step in the MapReduce Algorithm for matrix multiplication Facts. Number dot Product Or NoneNULL Description. J yi aij xj matrix elements accessed in row-major order repeated consecutive updates to yiwe can usually assume the compiler will optimize this also called inner product form since.
First we consider the parallelization of the operation on a linear array of processors when is a banded matrix with upper and lower bandwidths and we assume that matrices are stored using a sparse scheme For simplicity we describe the case. ClassToString int a. Dot Product Inputs.
Suppose we also have a vector v of length n whose jth element is vj. Matrix vector multiplication m number of slow memory references read x1n read y1n write y1n number of elements in one row of A num A rows m 3n n 2 f number of arithmetic operations 2n 2 multiply A and add y. Cm vector of m elements.
Matrix C aebg afbh cedg cfdh. We then use these results to compute Cs submatricies. UMSL Mathematics and Computer Science.
The above strategy is. ConsoleWriten Enter the number of rows in Matrix 1. If lenmat0 view the full answer.
Optical numerical analog processor for matrix-vector multiplication utilizing a computational architecture known as an engagement processor. Of columns in the first matrix should be equal to the no. Of rows in the second matrix.
ConsoleWriten Enter the number of columns in Matrix 1. Amn matrix of order mn bn vector of n elements Result. Refer To The Following Function Below That You Can Use Function Name.
Y i a ij x j y i 1 As a low arithmetic-intensity algorithm SpMV is typically bandwidth-bound and due to. An optimized algorithm splits those loops giving math6math algorithm. Program in C to multiply two matrices using Rectangular arrays.
Explain Matrix-Vector Multiplication Algorithm by MapReduce. We introduce matrices define matrix addition and scalar multiplication and prove properties of those operations. Row-sweep matrix-vector multiplication Row-major matrix-vector product y Ax where A is M N.
You dont write pseudo-code for the general matrix-matrix multiplication. Briefly described it is a variation of the systolic architecture proposed by Kung 1 for use in VLSI electronics. Sequential algorithm of matrix-vector multiplication In the given program code the following notation is used.
One column vector from matrix B. Matrix Multiplication We introduce matrix-vector and matrix-matrix multiplication and interpret matrix-vector multiplication as linear combination of the columns of the matrix. Matrix A a b matrix B e f c d g h There will be 8 recursive calls.
I yi 00. The only difference is that this Matrix Multiplication program in C uses functions to pass arrays of matrices. You pick one alg.
For the matrix multiplication to be visible the no.
Blocked Matrix Multiplication Malith Jayaweera
Computational Complexity Of Matrix Vector Product Mathematics Stack Exchange
Matrix Multiplication Calculator
Algorithms How To Find Vertices Of Bounded Region Made By Intersection Of Lines Computer Science Stack Exchange Vertex Planar Graph Algorithm
Pin On Mercedes Benz Wallpaper
Algorithms For Csr Based Sdmm To Compute The Multiplication Of Sparse Download Scientific Diagram
Parallel Matrix Vector Multiplication Algorithm Download Scientific Diagram
Parallel Matrix Vector Multiplication Algorithm Download Scientific Diagram
Pin On Algorithms Algorithmic Thinking
Numpy Vector Multiplication Geeksforgeeks
Two Fast Algorithms For Sparse Matrices Multiplication And
Mapreduce Algorithm For Matrix Multiplication
Pseudocode For Matrix Multiplication Download Scientific Diagram
Solved Structured Programming 40pts 3 Now That You Can Chegg Com
Introduction To Matrices And Matrix Arithmetic For Machine Learning
Pin On Adobe Illustrator Tutorials
Scalar Vector Multiplication Digital System Design
Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

