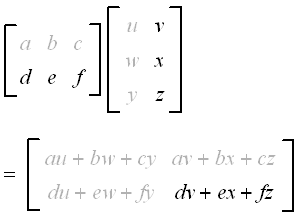Eigen Matrix Multiplication With Scalar

15 May, 2021

Eigen vector scalar multiplication. However it is necessary for the operations to be mathematically well-defined.

Part 22 Eigenvalues And Eigenvectors By Avnish Linear Algebra Medium

You should also consider defining mtx as an Array3Xf in the first place.

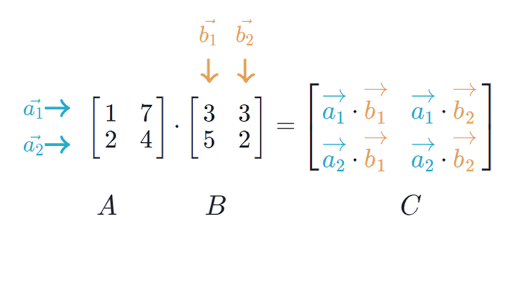
Eigen matrix multiplication with scalar. Typedef Matrix double 1 Dynamic RowVectorXd typedef Matrix double Dynamic 1 VectorXd. Take A x λ x and multiply by scalar k we get k A x k λ x. EigenMatrixXf C A 2.

Matrix and Scalar Arithmetic Eigen allows for straightforward addition and subtraction of vectors and matrices. Please consider the example provided here to understand this. Matrices interpret multiplication as matrix product and arrays interpret multiplication as coefficient-wise product.

Let A be an n n matrix and let X Cn be a nonzero vector for which AX λX for some scalar λ. Every square diagonal matrix is symmetric since all off-diagonal elements are zero. A slightly more verbose option would be.

Same as above without assigning the values to an additional Matrix. Array3Xf mtx EigenArray3XfOnes34. Where arrays are fundamentally different from matrices is when you multiply two together.

Answered Dec 3 15 at 442. This video demonstrates how to multiply a matrix by a scalar. EigenMatrixXf A 2 2.

But I guess this is the mistake you are making. The following are the typedefs defined in the documentation. Transpose matrix eigen c.

So with a scalar α 0 the eigenvalues are multiplied by α but the eigenvectors dont change. If is an eigenvalue of corresponding to the eigenvector then is an eigenvalue of corresponding to the same eigenvector. A k x λ k x Share.

The scalar is a fraction and fraction multiplication is discussed. But k A x A k x and k λ x λ k x so we see by definition that k x is an eigenvector. The set of all eigenvalues of an n n matrix A is denoted by σA and is referred to as the spectrum of A.

If we multiply a matrix by a scalar then all its eigenvalues are multiplied by the same scalar. This scalar multiplication of matrix calculator can help you when making the multiplication of a scalar with a matrix independent of its type in regard of the number of rows and columns. If we expand this idea from vectors to matrices most matrices can be decomposed into a matrix of column eigenvectors P and a diagonal matrix D that is filled with eigenvalues on the main diagonal.

If you multiply a column vector to a column vector you will get the result what you are getting as question details are not much clear. We can not of course say that a matrix is equivalent to a single scalar value but when multiplying a matrix by one of its eigenvectors then the matrix may be replaced by a scalar its eigenvalue. What an incredibly fantastic simplification.

In addition they must also possess the same scalar type. Matrix multiplication c eigen Code Answers. The corresponding eigenvalue often denoted by is the factor by which the eigenvector is scaled.

Scale the matrix values by 2. All operations involving vectors are just the special case of Nx1 matrix. Conversely if λ is an eigenvalue of α A with eigenvector v then we have that α 1 v is an eigenvector relative to λ for α 1 α A A.

Many problems allow us to represent a matrix in terms of its eigenvalues and eigenvectors. In linear algebra a real symmetric matrix represents a self-adjoint operator over a real inner product space. The two operands must have the same number of rows and columns.

Proposition Let be a matrix and a scalar. Cpp by Breakable Booby on Jun 08 2020 Donate Comment. For all indices and.

First of all of course you can multiply an array by a scalar this works in the same way as matrices. If the scalar is 0 then α A is the zero matrix having only the zero eigenvalue. You can multiply a matrix with a vector as long as the rules of matrix-vector multiplication.

In linear algebra an eigenvector ˈaɪɡənˌvɛktər or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. Then λ is called an eigenvalue of the matrix A and X is called an eigenvector of A associated with λ or a λ -eigenvector of A. Definition EEM Eigenvalues and Eigenvectors of a Matrix Suppose that A A is a square matrix of size n n x0 x 0 is a vector in Cn C n and λ λ is a scalar in C C.

The scalar multiplication with a matrix requires that each entry of the matrix to be multiplied by the scalar. 1 matrix multiplication c eigen. Remember that for an eigenvector multiplication with the transformation matrix A is equivalent to multiplying with a simple scalar λ.

Similarly we can multiply and divide by a scalar variable. The matrix can have from 1 to 4 rows andor columns. Then we say x x is an eigenvector of A A with eigenvalue λ λ if Axλx A x λ x Before going any further perhaps we should convince you that such things ever happen at all.

A. Element-wise operations with Eigen are best done in the Array domain. Similarly in characteristic different from 2 each diagonal element of a skew-symmetric matrix must be zero since each is its own negative.

α A v α λ v λ α v This shows that α v 0 is an eigenvector relative to λ for α A. Here is a short proof.

7 1 Introduction To Eigenvalues And Eigenvectors Applied Data Analysis And Tools

Pin On Mechanics

Pin On Linear Algebra Videos

Multiplying Matrices Article Matrices Khan Academy

4 Multiplication Of Matrices

Part 22 Eigenvalues And Eigenvectors By Avnish Linear Algebra Medium

How Do I Make My Matrix Object Implicitly Convert To Scalar When Its Dimensions Are 1x1 Stack Overflow

Multiplication Of 3x3 Matrices Matrix Multiplication Youtube

What Does Span Mean In Linear Algebra Algebra Linear Math

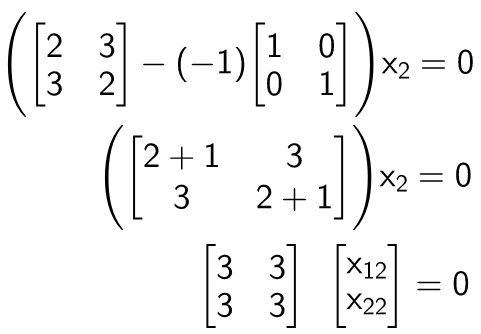
Part 22 Eigenvalues And Eigenvectors By Avnish Linear Algebra Medium

Ndsru9npbulyrm

Matrices Vectors And 3d Math A Game Programming Approach With Matlab By Scott Stevens Click The Pin To Visit The Store P Matrices Math Math Math Textbook