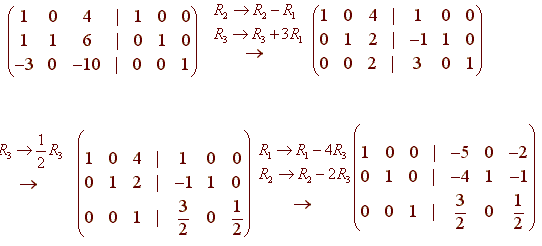If We Multiply A Matrix By Its Inverse We Obtain

When we multiply a number by its reciprocal we get 1. Both sides of that equation are undefined unless A is 1 1.

Multiplicative Inverses Of Matrices And Matrix Equations Video Lesson Transcript Study Com

Adding times the third row of the matrix to its second row we obtain the matrix.

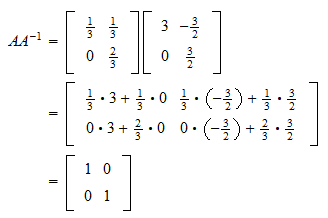
If we multiply a matrix by its inverse we obtain. Inverse of A is denoted by. Where is a real number. Whether we add and then subtract this is EE 1.

Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. The inverse is not possible with just any kind of matrix a matrix must be square and invertible and the reasons are explained in this article along with several identities and examples involving inverse matrices. In fact if as an example we give the value of and take the first matrix form we will obtain the matrix that we have checked to be orthogonal above in the section Example of a 22 orthogonal matrix.

If instead A is a complex square matrix. Using determinant and adjoint we can easily find the inverse of a square matrix. If you have a number such as 32 and its inverse in this case 23 and you multiply them you get 1.

Multiply EE 1 to get the identity matrix I. We are adding and subtracting the same 5 times row 1. If A is invertible then the factorization is unique if we require the diagonal elements of R to be positive.

Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. The Inverse of a Square Matrix 853 Comments We must left multiply both sides of AX B by A 1. Think back to the nature of inverses for regular numbers.

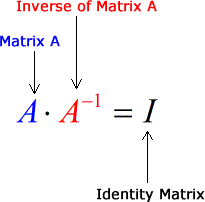
If you multiply a matrix and its inverse you get the identity matrix I. Xrightarrow X is injective then fx Lx as above has an inverse g that is defined everywhere on X which forces fcirc gyy for all y in Y. When we multiply a matrix by its inverse we get the Identity Matrix which is like 1 for matrices.

The inverse of a matrix A is written as A 1 so A A - 1 I. Example Consider the system of two equations in two unknowns The system can be written in matrix form as where If we multiply the first equation by and leave the second equation unchanged we obtain a new system The matrix form of the new system is where The new system is equivalent to the original one because the same result can be achieved by pre-multiplying the matrix form of the original system by. In other words if M is a matrix such that MLI on the finite dimensional linear space X then it.

18 8 1. Properties of an orthogonal matrix. Ie AT ij A ji ij.

A A -1 I. An orthogonal matrix can never be a singular matrix since it can always be. Cases and definitions Square matrix.

Any real square matrix A may be decomposed as where Q is an orthogonal matrix its columns are orthogonal unit vectors meaning and R is an upper triangular matrix also called right triangular matrix. When we multiply a number by its reciprocal we get 1 and when we multiply a matrix by its inverse we get Identity matrix. The inverse is used to find the solution to a system of linear equation.

E D 2 4 100 510 001 3 5 and E 1 D 2 4 100 510 001 3 5. Fortunately the division is possible when a matrix is multiplied with its inverse which is unique. Since we know that the product of a matrix and its inverse is the identity matrix we can find the inverse of a matrix by setting up an equation using matrix multiplication.

Finding the Multiplicative Inverse Using Matrix Multiplication Use matrix multiplication to find the inverse of the given matrix. Also multiply E 1E to get I. It works the same way for matrices.

A -1 A I. If the result of multiplying a matrix A by another matrix is the identity matrix I then the second matrix is the inverse of matrix A. Example 2 Inverse of an eliminationmatrixIfE subtracts 5 times row 1 from row 2 then E 1 adds 5 times row 1 to row 2.

Remember that matrix multiplication is not commutative. The characteristics of this type of matrix are. Same thing when the inverse comes first.

The product of original and inverse matrix gives identity matrix A x A inverseidentity Post multiplying by A inverse Aidentity x A inverse Do matrix multiplication and get the answer. If we were to right multiply then we would obtain AXA 1 BA 1. Adding times the third row of the matrix to its first row we obtain the matrix.

Multiplying the third row of the matrix by we obtain the matrix. And 1 is the identity so called because 1x x for any number x. 8 18 1.

Therefore if L.

Inverse Matrix

6 4 Inverse Matrices

When A Matrix Is Multiplied By Its Inverse Why Is The Answer An Identity Matrix And Not A Unit Matrix Quora

Pin On Education

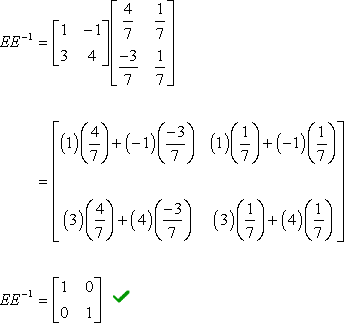
Inverse Of A 2x2 Matrix Chilimath

Inverse Of A Matrix

Pin On Algebra

Pin On Study

Pin On 10 Math Problems

Pin On High School Math

Inverse Of A 2x2 Matrix Chilimath

Pin On Matematicas

Inverse Matrices And Their Properties Youtube

Question Video Finding An Unknown Matrix In An Equation Using The Inverse Of A Matrix Nagwa

Lesson Video Properties Of Inverse Matrices Nagwa

Question Video Finding An Unknown Matrix In An Equation Using The Inverse Of A Matrix Nagwa

Inverse Of A 2x2 Matrix Chilimath

Pin On Math

Pin On 10 Math Problems