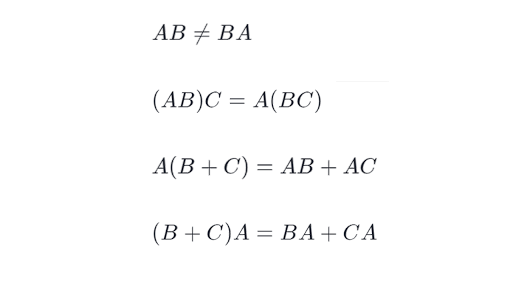Matrix Multiplication Abelian Group
Here are some basic. DetA 6524 22 1 mod 7.

Chapter 3 Groups 10 Prove That The Set Of Matrices Chegg Com
Closuretotality any two elements of the group can be multiplied to get another element of the group associativity identity and inverses.
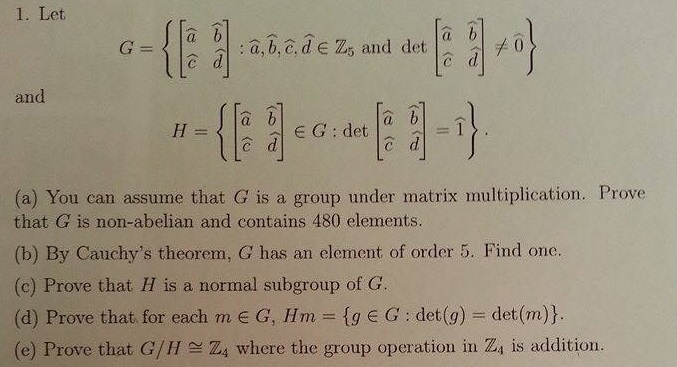
Matrix multiplication abelian group. φ cos θ-sin θ sin θ cos θ e iθ. Is matrix multiplication Abelian group. For an order two element we can take 0 1 1 0.
Where j J J G the m x n integer Xl x n by m relations r I r 2 o. R m 0 the ai j are integers then there is associated with matrix A aij known as a relation matrix of G. In fact it has degree m2 and if m is prime to the characteristic.
Is a group under matrix multiplication. In SL2Z 7 consider A 6 2 4 5. Here the identity is the matrix 1 2 1 0 0 1 The existence of inverses is part of the de nition.
There are infinitely many subfields of R and therefore are infinitely many subgroups of. The zero matrix has no inverse. Multiplication is associative since matrix multiplication is associative.
By definition consists of invertible matrices so every element has a multiplicative inverse. Under matrix multiplication but not a group since this set includes many singular matrices. It is a non-Abelian group.
Here the group operation on G is matrix multiplication and the group operation on G 0 is the multiplication of complex numbers. Is matrix multiplication reversible. You should know from linear algebra that matrix multiplication is not commutative.
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. For every integer m multiplication by m on E is a endomor-phism of E which we will denote by m. The set Mn R of all n n real matrices with addition is an abelian group.
The group is abelian if and only if this table is symmetric about the main diagonalie. If m 6 0 then the endomorphism m is nonzero. The associativity of matrix multiplication is not entirely.
Ab 1 a 1b 1 for all ab 2G G is Abelian. Because G is Abelian b 1a 1 a 1b 1. In contrast the group of invertible matrices with a group law of matrix multiplication do not form an abelian group it is nonabelian because it is not generally true that M N N M MN NM M N N M for matrices M N MN M N.
It is in fact the group of units of M 2R It is not abelian. G be an additively written abelian group defined on n generators n If ri I a. Each element in G 0 is equal to e iθ for some θ R.
To verify that a finite group is abelian a table matrix - known as a Cayley table - can be constructed in a similarfashion to a multiplication table. It is then straightforward to prove the following facts using only what you know about matrix multiplication. An endomorphism of E is also a homomorphism of the abelian group structure on E see Si Theorem III48.
10 Let p be prime and F 2 QRCZ p. If the group is G g1 e g2 gn under the operation the i jth entry of thistable contains the product gi gj. If the matrix is a symmetric matrix.
Note that a 1b 1 ba 1. Therefore ab 1 ba 1. The special linear group SL2F is SL2F a b c d abcd 2 Fadbc 1 where the operation is matrix multiplication modulo p in Z p.
The required axioms matrix multiplication must satisfy to be a group operation the operation is not the whole group are. However Mn R with matrix multiplication is NOT a group eg. If X A X and X B X for some 2 2 matrices A and B then also X.
We already know that matrix multiplication is associative that the product of two invertible matrices is invertible that the identity matrix is 1 0 0 1 The inverse of a b c d is 1 ad bc d b c a So GL 2Ris a group. G A M 2 2 R det A 0 X A X. The even integers under multiplication form an abelian semigroup that is not a monoid since it contains.
A1 5 2 4 6. Thus ab ab 1 1 ba 1 1 ba and G is Abelian. G- G 0 as follows.
The symmetric group S n S_n S n is also nonabelian for n 3 n geq 3 n 3. G is Abelian ab 1 a 1b 1 for all ab 2G. Note that ab 1 b 1a 1 in general.
To work with homotopies in a simplicial complex one can find a non-Abelian group called fundamental group described by certain relations and assign to each 1-simplex an element of the group such that deciding if a path is contractible amounts to testing whether the product of the corre-sponding group elements is the identity. φ is a bijective group homomorphism. With the situation is reversed.
Let X be the 1 2 matrix X 1 1 a vector if you prefer. 25Prove that a group G is Abelian if and only if ab 1 a 1b 1 for all a and b in G. This translation group is Abelian.
Find an abelian subgroup. The set GL2R of invertible 2-by-2 real matrices with group law matrix multiplication is a non-abelian group. Define a map φ.
The nonzero elements of Q R and C form infinite abelian groups under multiplication denoted Q R and C respectively. Matrix multiplication is associative and the identity is the identity matrix. The inverse of a b c d is d b c a.
If F is a subfield of R see below then the group of invertible matrices with coefficients in F is a subgroup of G.
Properties Of Matrix Multiplication Article Khan Academy

Solved Consider The Following Set Of Real 2 X 2 Matrices Chegg Com

Lecture 3 Example Of A Group With Matrix Multiplication Youtube

Abstract Algebra 1 Definition Of An Abelian Group Youtube

Approaches To Bounding The Exponent Of Matrix Multiplication

Prove That The Set Of Matrix 2x2 Under Matrix Multiplication As Commutative Group Youtube

Is Matrix Multiplication Commutative Video Khan Academy
Matrix Multiplication From Wolfram Mathworld

Associative Property Of Matrix Multiplication Video Khan Academy
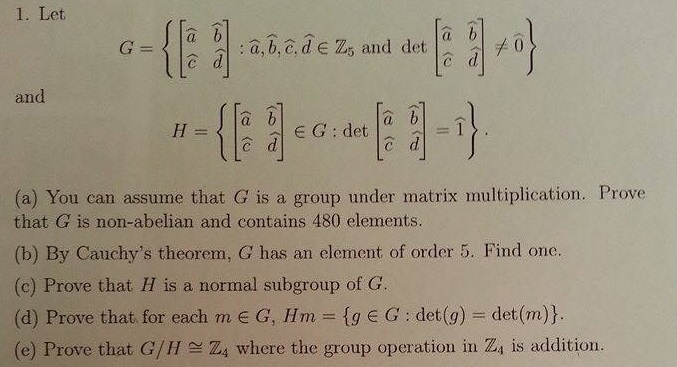
Let G You Can Assume That G Is A Group Under Matrix Chegg Com

Matrix Multiplication Algorithm Wikiwand

Consider The Following Set Of Real 2 2 Matrices A Chegg Com

Solved 1 Consider The Following Sets Of Real 2 2 Matrice Chegg Com

Sign In Or Register Studying Math Matrix Multiplication Teaching Math

Sign In Or Register Matrix Multiplication Properties Of Multiplication Multiplication

Let M Be The Set Of 2 X 2 Matrices Of The Form 82 Chegg Com

Sign In Or Register Matrix Multiplication Theorems Algebra