Matrix Multiplication Complexity
In the above method we do 8 multiplications for matrices of size N2 x N2 and 4 additions. In particular matrix multiplication the main concepts in low degree algebraic complexity theory have been introduced for the study of the complexity of matrix multiplication Algebraic complexity theory.

Strassen S Matrix Multiplication Algorithm When N Is Not A Power Of 2 Computer Science Stack Exchange
It should be noted that the above function computes the same subproblems again and again.

Matrix multiplication complexity. Θn28074 Best case time complexity. 2 Calculate following values recursively. The naive matrix multiplication for A B involves multiplying and adding N terms for each of M P entries in A B.
Worst case time complexity. Calculate the 7 matrix multiplications recursively. Up to 10 cash back The matrix multiplication complexity of text Mat_ ntimes ntimes n is the lowest computational complexity of evaluating the bilinear mapping text Mat_ ntimes ntimes n ie multiplying any two given ntimes n matrices in F ntimes n which is counted by the number of multiplications required to compute their matrix multiplication.
Combine these submatricies into our new matrix C. 1 Divide matrices A and B in 4 sub-matrices of size N2 x N2 as shown in the below diagram. However it is unknown what the underlying complexity actually is.
The naive algorithm has complexity Omjn for multiplying an m x j matrix by a j x n matrix or On3 for square n x n matrices. And then multiplying this M P matrix by C requires multiplying and adding P terms for each of M N entries. I took 2 2 and 3 3 matrices and I extended the same concept to nn.
Minimum number of multiplications is 30 The time complexity of the above naive recursive approach is exponential. See the following recursion tree for a matrix chain of size 4. See the wikipedia article on matrix multiplication.
For example if you multiply a matrix of. It will not be O n2 in the general case. For multiplying the two 22 dimension matrices Strassens used some formulas in which there are seven multiplication and eighteen addition subtraction and in brute force algorithm there is eight multiplication and four addition.
The standard way of multiplying an m-by-n matrix by an n-by-p matrix has complexity O mnp. So the total complexity is. Study of computation using algebraic models.
Ae bg af bh ce dg and cf dh. The best known algorithm has complexity approximately On23728639. About the method The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of.
If all of those are n to you its O n3 not O n2. Following is simple Divide and Conquer method to multiply two square matrices. A nparray 123 456 B nparray 123 456 print Matrix A isnA print Matrix A isnB C npmultiply AB print Matrix multiplication of matrix A and B isnC The element-wise matrix multiplication of the given arrays is calculated in the following ways.
Enjoy the videos and music you love upload original content and share it all with friends family and the world on YouTube. But there are faster algorithms for particular types of matrices -- if you know more you may be able to do better. In this I explained how to compute the complexity of the matrix multiplication.
Compute the submatricies of C. So the complexity is O N M P. The utility of Strassens formula is shown by its asymptotic superiority when order n of matrix reaches infinity.
As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the.

Time Complexity Of Matrix Multiplication In Big Align Computer Science Stack Exchange

Systolic Arrays Algorithm For Matrix Multiplication Mathematics Stack Exchange

2 9 Strassens Matrix Multiplication Youtube

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Strassen S Matrix Multiplication Divide And Conquer Geeksforgeeks Youtube

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm

Table I From A Lut Based Matrix Multiplication Using Neural Networks Semantic Scholar

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Matrix Chain Multiplication Dynamic Programming Youtube
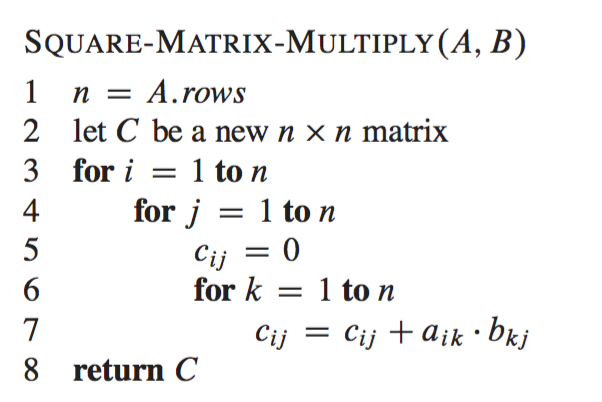
Matrix Multiplication Using The Divide And Conquer Paradigm
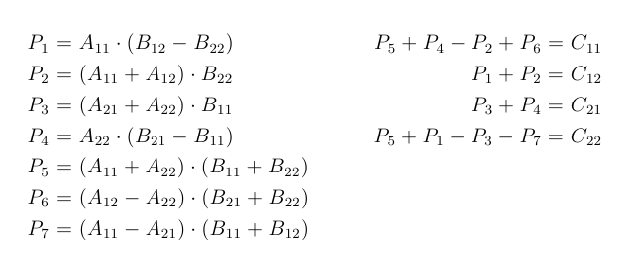
Strassen Matrix Multiplication C The Startup
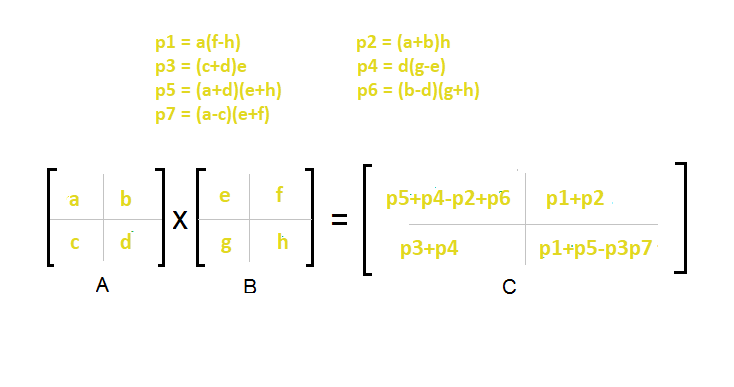
Strassen S Matrix Multiplication Algorithm

Tuning Strassen S Matrix Multiplication For Memory Efficiency

Strassen S Matrix Multiplication
Strassen S Matrix Multiplication Algorithm

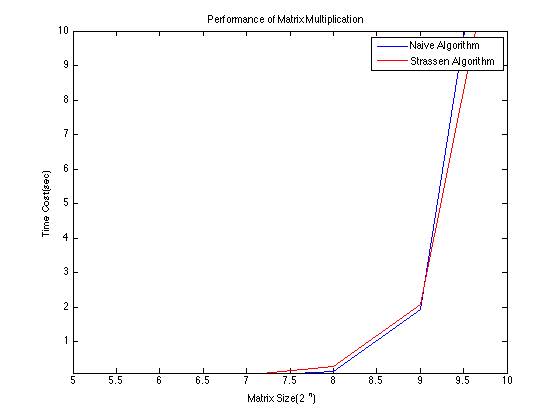
Complexity Of Various Algorithms For Matrices Multiplication 9 10 11 Download Table

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
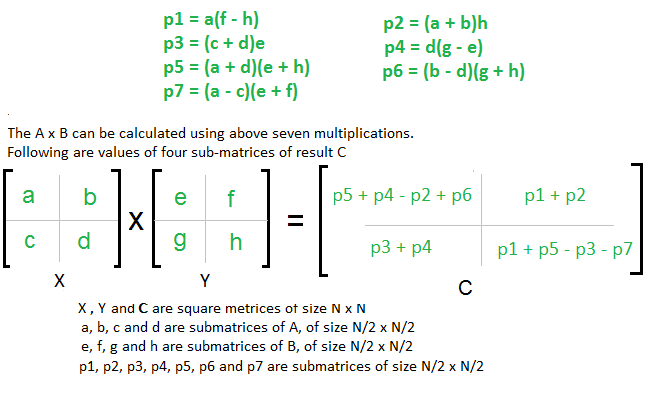
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks
