Matrix Multiplication Minimum Operations
Int first 1010 second 1010 multiply 1010. Best Most Votes Newest to Oldest Oldest to Newest.
1 2 3 4.

Matrix multiplication minimum operations. PrintfEnter number of rows and columns of first matrixn. Max_val 99999999 Number of matrices N lenp -1 We want to return M1N as the optimal cost of product of multiplying 1N matrices M 0 N 1 for r in range N 1. June 17 2020 139 PM.
Output Minimum number of matrix multiplication. N dimslength - 1. 30000 There are 4 matrices of.
What is the minimum operations to multiply all these three matrices. Scanfdd. Multiply the number by 3.
MatrixChainMultiplication int dims. M ij Minimum number of scalar multiplications ie cost needed to compute the matrix A iA. Lots of research has been done on multiplying matrices using a minimum number of operations.
About the method The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one. The multiplication sequence parenthesization is important. August 10 2020 1205 AM.
Mr 0 N 1 Multiplications needed for a single matrix. 5 A big difference. Here the result is 18.
Multiply the number by 2. D scanfd. The minimum number of multiplications are obtained by putting parenthesis in following way A BCD -- 203010 402010 401030 Input.
The operations that can be performed in one step are as follows. Length dims n 1. Algorithm matOrderarray n Input List of matrices the number of matrices in the list.
Minimum number of operations need multiply these three matrices. 2 3 3 4. As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the.
It means the matrices are 1 x 2 2 x 3 3 x 4. Below function computes the minimum number of multiplications needed to find the product of the chain of matrices in bottom up fashion def ChainMultiplication p. Can you please explain how did you figured.
Doing a ktimes l times ltimes m matrix multiplication in the straightforward way every entry of the result is a scalar product of of two l-vectors which requires l multiplications and l-1 additions. Require at minimum k-times the duration of an n x n n x n Matrix Multiply if the same matrix multiplication algorithm was applied to both calculations. Direct Matrix multiplication of Given a matrix a matrix and a matrix then can be computed in two ways and.
Matrix multiplication is repeatedly used in programs to represents a graphical data structure which is used to store multiple vectors and also it is used in many applications like solving linear equations and more. C for d 0. 5 When 1 and then.
Let the input 4 matrices be A B C and D. The number of multiplications needed are. P 10 20 30 40 30 Output.
The orders of the input matrices. PrintfEnter elements of first matrixn. For c 0.
Add 1 to the number.

This Lesson Is Designed To Open Up A Discussion For Algebra 2 Students Related To A Trigonometry Unit Students Will Begin To Algebra We Are Teachers Algebra 2

Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium

Minimum Number Of Jumps To Reach End
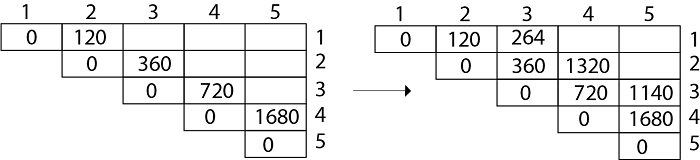
Matrix Chain Multiplication Using Dynamic Programming By Chetan More Medium
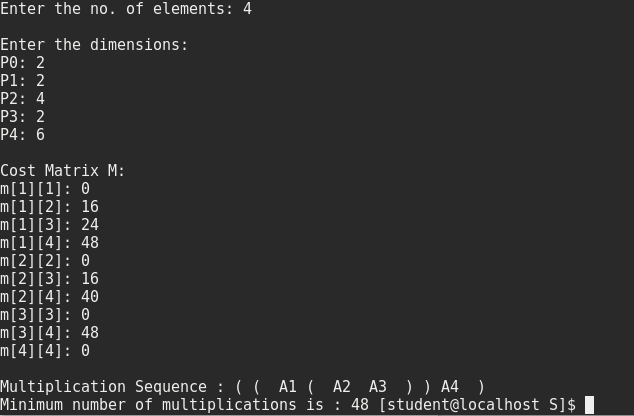
Matrix Chain Multiplication With C Program Example Random Access Memories

Program To Implement Stack Using Linked List Linked List Stack Pep

Find Minimum Cost To Reach The Last Cell Of A Matrix From Its First Cell Techie Delight

Http Www Aplustopper Com Minimum Maximum Values Function How Do You Find Function Maxima

Minimum Operations To Reduce X To Zero O N Optimal Leetcode 1658 Youtube

4 3 Matrix Chain Multiplication Dynamic Programming Youtube

Matrix Chain Multiplication Dynamic Programming Youtube
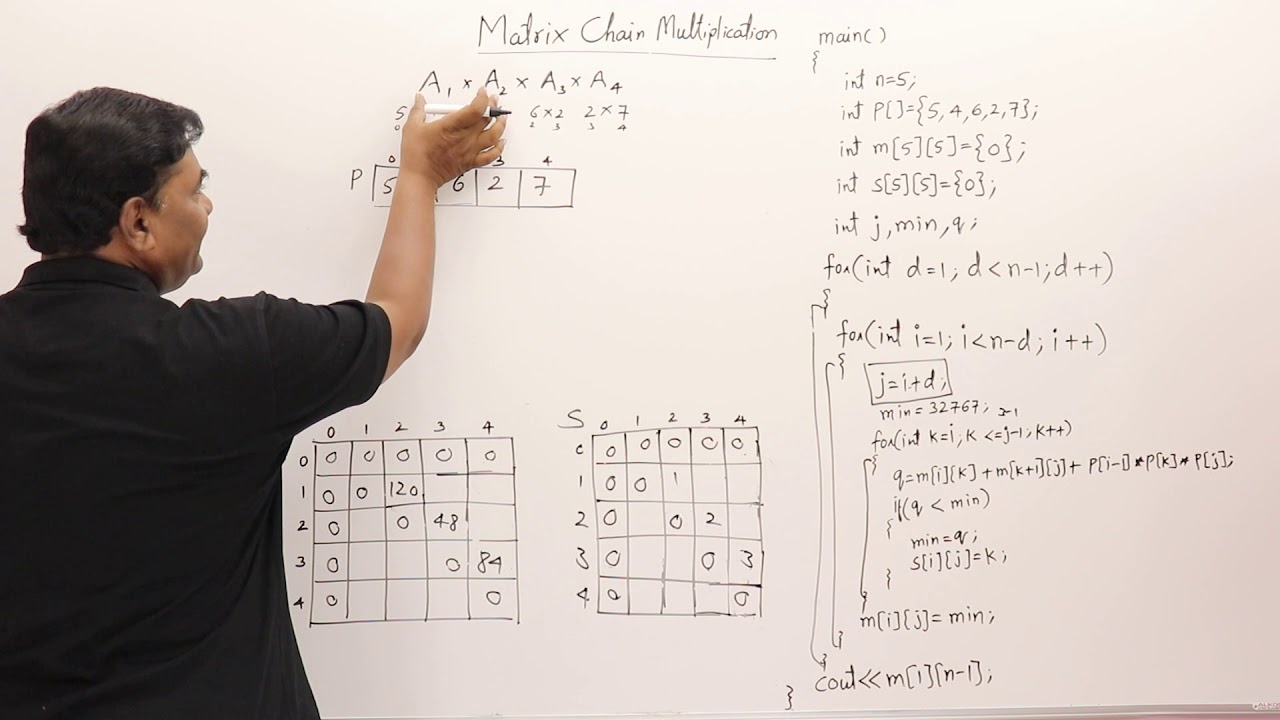
4 3 Matrix Chain Multiplication Dynamic Programming Youtube

Find The Minimum And Maximum Amount To Buy All N Candies Geeksforgeeks

Minimum Number Of Jumps To Reach End




