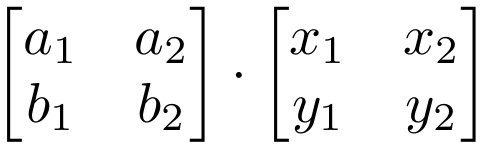Rotation Matrix Dot Product
Barv cdot bark barv cdot bark cdot cos theta Where the angle between them is represented as theta theta. Let us suppose we have unit vectors u v R m with u v.
Multiplication of Rotation Matrices Recall from above that the dot product of any two different rows or columns of a rotation matrix is zero while the dot product of any row or column with itself is one.

Rotation matrix dot product. A A RT Also you can arrange the transformation in the standard form rotation matrix first by taking the transpose of A prior to the multiplication then transposing the result. Rather this article demonstrates in C three of the core linear algebra concepts matrix multiplication dot product and transformation matrices. The invariance of dot products implies that both the lengths of vectors and the angle between vectors are unchanged in a rotation.
This can be written in matrix and tensor notation as R RT I and RikRjk δij R R T I and R i k R j k δ i j. First the syntax of the matrix multiplication can be slightly simplified using the recently added matrix multiplication operator. Rotations and Angular Velocity A rotation of a vector is a change which only alters the direction not the length of a vector.
DotColumn int j Vector4 v double Returns the dot product of column j and v. Grab the top row of the square matrix and rotate it clockwise by 90 degrees align the entries with those of the column matrix and multiply corresponding entries add all of these products together place this sum at the top of a new column matrix. Rotation matrix in terms of dot products.
Determinant double Returns the determinant of this matrix. This can be written in matrix and tensor notation as QQT I. Here θ is the angle between the vectors A and B when they are drawn with a common origin.
Cos sin sin cos z R x y z v xcos ysin ycos xsin 514 This dot product rotates the vector in the counter-clockwise direction about the origin by an angle as shown in Figure 54. Multiplication of Transformation Matrices Recall from above that the dot product of any two different rows or columns of a transformation matrix is zero while the dot product of any row or column with itself is one. Therefore preserving the length of vectors implies that dot products are invariant.
1 dot prod divide by the lengths normas and you get ccos alpha 2 cross prod divide by the lengths normas and you get ssin alpha 3 atan2 gives you alpha atan2 sc Note that atan2 is as speedy as the acos you used I suppose. A rotation consists of a rotation axis and a rotation rateBy taking the rotation axis as a direction and the rotation rate as a length we can write the rotation as a vector known as the angular velocity vector vecomega. Source Code Source code for this article is available on GitHub on the following repository.
If this sounds confusing take a look at its formula. A property or rotations is that their matrices are orthogonal and their transpose is equal to their inverse so that R t R 1 so the scalar product is u R R 1 v t and R R 1 I the identity matrix so that u R R t v t u R R 1 v t u I v t u v t ie. DotRow int i Vector4 v double Returns the dot product of row i and v.
Scalar product Dot product This product involves two vectors and results in a scalar quantity. Lets use the fact that dot products are invariant to derive a property of the rotation matrices. Decomposes this into translation rotation and scale components.
Let T u v denote the unique rotation of R m carrying u to v and which is the identity on the orthogonal complement of Span u v. The dot product of two vectors is equal to the scalar product of their lengths times the cosine of the angle between them. A useful example is the dot product of two-dimensional rotation matrix R with a coordinate vector v xyt.
The dot product is invariant under rotation. In the previous lesson we became familiar with the concept of the configuration for the robots and we saw that the configuration of a robot could be expressed by the pair Rp in which R is the rotation matrix that implicitly represents the orientation of the body frame with respect to the reference frame and p is the position of the origin of the body frame relative to the space frame. The scalar product between two vectors A and B is denoted by A B and is defined as A B AB cos θ.
That close association is why one still sees ı ȷ and k as the canonical unit vectors. Entry int row int col double Value at row col. Historically the dot product and cross product as used by physicists on vectors in ℝ 3 are much more closely associated with the quaternions that the concept of vector spaces in general bivectors and the wedge product.

The Matrix Representation Of Any 2nd Order Tensor That Has Been Generated From The Tensor Product Of Any Two Vectors Wil Studying Math Logic Math Matrices Math
Matrix Multiplication Calculator

Circular Rotation Around An Arbitrary Axis Stack Overflow

Maya Tutorial How To Place Correctly The Polevector With Python Pt2 Tutorial Python Maya
Opengl Rotation About Arbitrary Axis

Pin On Ncert Solutions For Class 12 Maths

Dot Product Explained Vector Calculus Calculus Mathematics Geometry
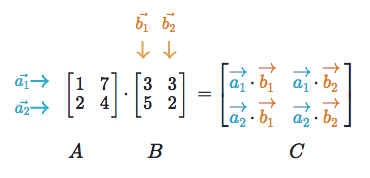
Linear Algebra Ml Glossary Documentation

Describing Rotation In 2d Robot Academy

Calculate Rotation Matrix To Align Vector A To Vector B In 3d Programmer Sought