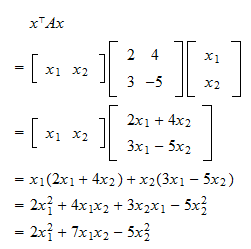Symmetric Matrix Eigenvalues Positive

Positive Eigenvalues Proposition Let A be a real symmetric matrix. X TAx yT zx QΛ y zQTx yTΛy X i λ iy 2 i For x 60 we have y 60 and thus xTAx P i λy2 0.

For A Symmetric Positive Definite Matrix Why Does Each Diagonal Element Exceeds The Small Eigenvalue Mathematics Stack Exchange

The determinant of a positive definite matrix is always positive but the de.

Symmetric matrix eigenvalues positive. Enter your answers as a comma-separated list. The first condition implies in particular that which also follows from the second condition since the determinant is the product of the eigenvalues. A λI λ2 8λ 11 0 ie.

Hence A is positive definite. However they are not necessarily all positive. X T A x 0 for all non zero vector x.

Symmetric Matrix with Positive Eigenvalues. Then hAxxi x2 1 x22 is not nonnegative for jx 1j. For example consider matrix.

All of the eigenvalues of a variance-covariance matrix. M is symmetric or Hermitian and all its eigenvalues are real and positive resp. Every leading principal minor where the submatrix comprises the intersection of rows and columns to is positive the eigenvalues of are all positive.

Consider the quadratic form of A. A Prove that the eigenvalues of a real symmetric positive-definite matrix A are all positive. The determinant of a positive definite matrix is always positive but the de terminant of 0 1 3 0.

Note that as its a symmetric matrixall the eigenvalues are real so it makes sense to talk about them beingpositive or negative. A symmetric matrix A is positive semidefinite if and only if all of its eigenvalues are 0. In the latter case A is also nonsingular.

Conversely suppose that all the eiganvalues of A are positive. We say a symmetric matrix Mis positive semide nite PSD if all eigenvalues of Mare nonnegative. If A is positive definite and λ is an eigenvalue of A then for any eigenvector x belonging to λ xAxλxx λkxk2.

Its eigenvalues are the solutions to. The eigenvalues of A are real numbers. We usually use the notation M 0 to denote that M is PSD.

Hence λ xAx kxk2 0. A matrix M is positive-definite resp. The matrix is symmetric and its pivots and therefore eigenvalues are positive so A is a positive definite matrix.

A 1 3 0 1. Not all matrix with positive eigenvalues is positive definite ie. In particular any PSD matrix M can be.

Let A 1 2 2 1. If A is symmetric and has positive eigenvalues then by the spectral theorem for symmetric matrices there is an orthogonal matrix Q such that A Qtop Lambda Q with Lambda textdiaglambda_1dotslambda_n. M is congruent with a diagonal matrix with positive resp.

A λI 2 λ 8λ 11 0 ie. A is positive definite if and only if all of its eigenvalues are 0. X For each eigenvalue find the dimension of the corresponding eigenspace.

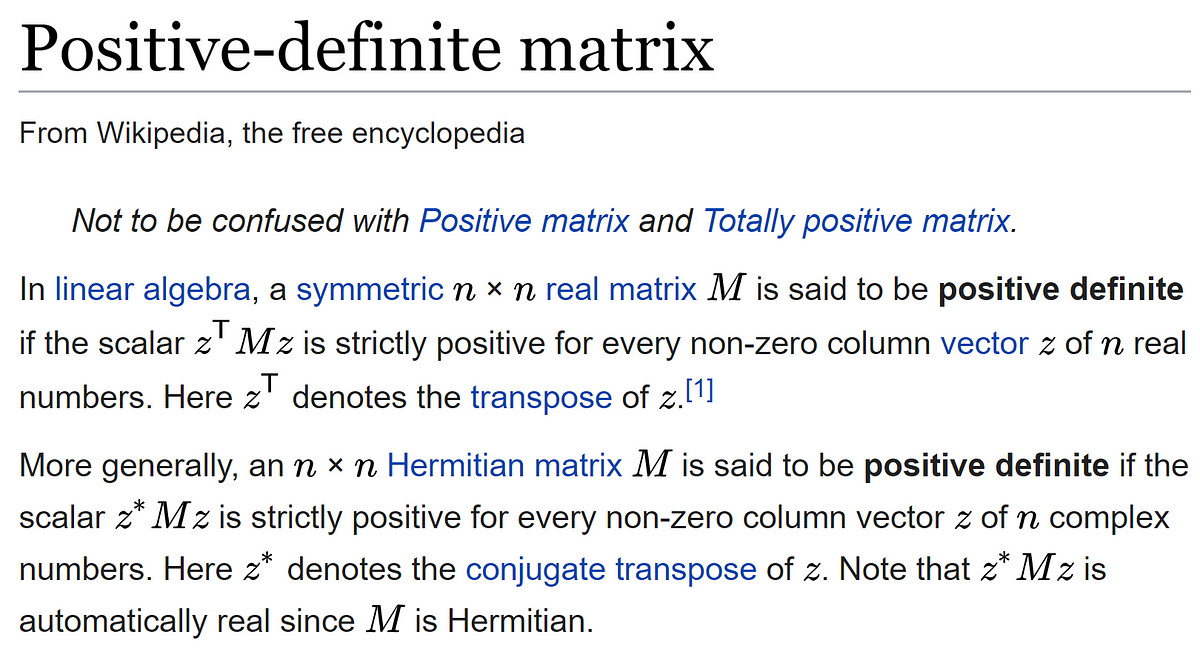
If x is any nonzero vector then y Qx ne 0 and. Positive definite Real Symmetric Matrix and its Eigenvalues A real symmetric n n matrix A is called positive definite if xTAx 0 for all nonzero vectors x in Rn. Find the eigenvalues of the symmetric matrix.

They are all real. If every eigenvalue of A is positive then A is positive definite. Note that applying the complex conjugation to the identity Aviw aibviw yields Av iw a ibv iw.

4 5. Symmetric matrices have real eigenvalues The Spectral Theorem states that if Ais an n nsymmetric matrix with real entries then it has northogonal eigenvectors. Then A is positive definite if and only if all its eigenvalues are positive.

By the spectral theorem we have A QΛQT where Q is orthogonal. Its eigenvalues are the solutions to. The matrix property of being real and symmetric alone is not sufficient to ensure that its eigenvalues are all real and positive.

A positive definite matrix is a symmetricmatrix with all positive eigenvalues. A symmetric matrix is positive semide nite if and only if its eigenvalues are nonnegative. The matrix is symmetric and its pivots and therefore eigenvalues are positive so A is a positive definite matrix.

1 x22 0 implying that Ais positive semide nite. The rst step of the proof is to show that all the roots of the characteristic polynomial of Aie. According to Theorem 823 all the eigenvalues of K are real and positive and so the eigenvalues of the negative definite.

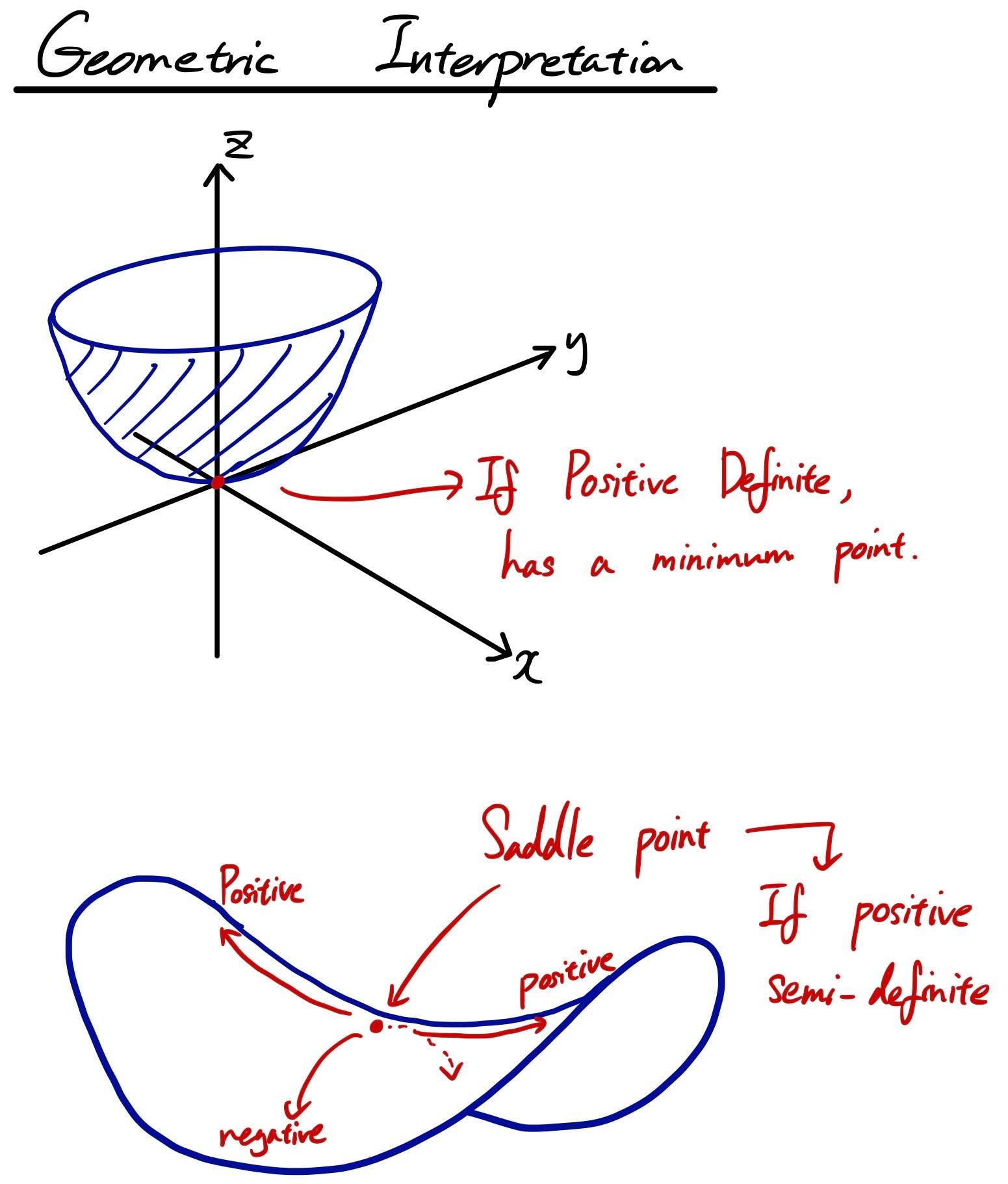
B Prove that if. In order for a matrix to have all real and positive eigenvalues it must possess one. Today were going to talk about a special type of symmetric matrixcalled apositive definitematrix.

Positive-semidefinite if and only if satisfies any of the following equivalent conditions. Theorem 11 Let A be a real nn symmetric matrix. Hence Ais not positive semide nite.

Enter your answers from smallest to largest 03 03 3 3 3 i. Suppose v iw 2 Cn is a complex eigenvector with eigenvalue aib here vw 2 Rn. It remains to show that if aib is a complex eigenvalue for the real symmetric matrix A then b 0 so the eigenvalue is in fact a real number.

For a positive semide nite Mwe can write p M M12 Xn i1 p iv iv i. A particularly important class of systems are the linear gradient flows in which AT is a symmetric positive definite matrix. The following is a ready consequence.

Show that if Ais positive semide nite then every diagonal entry of Amust be nonnegative.

Determine If The 2x2 Matrix Is Positive Definite And Then Find The Cholesky Decomposition And An Ort Youtube

How To Prove That A Matrix Is Positive Definite Youtube

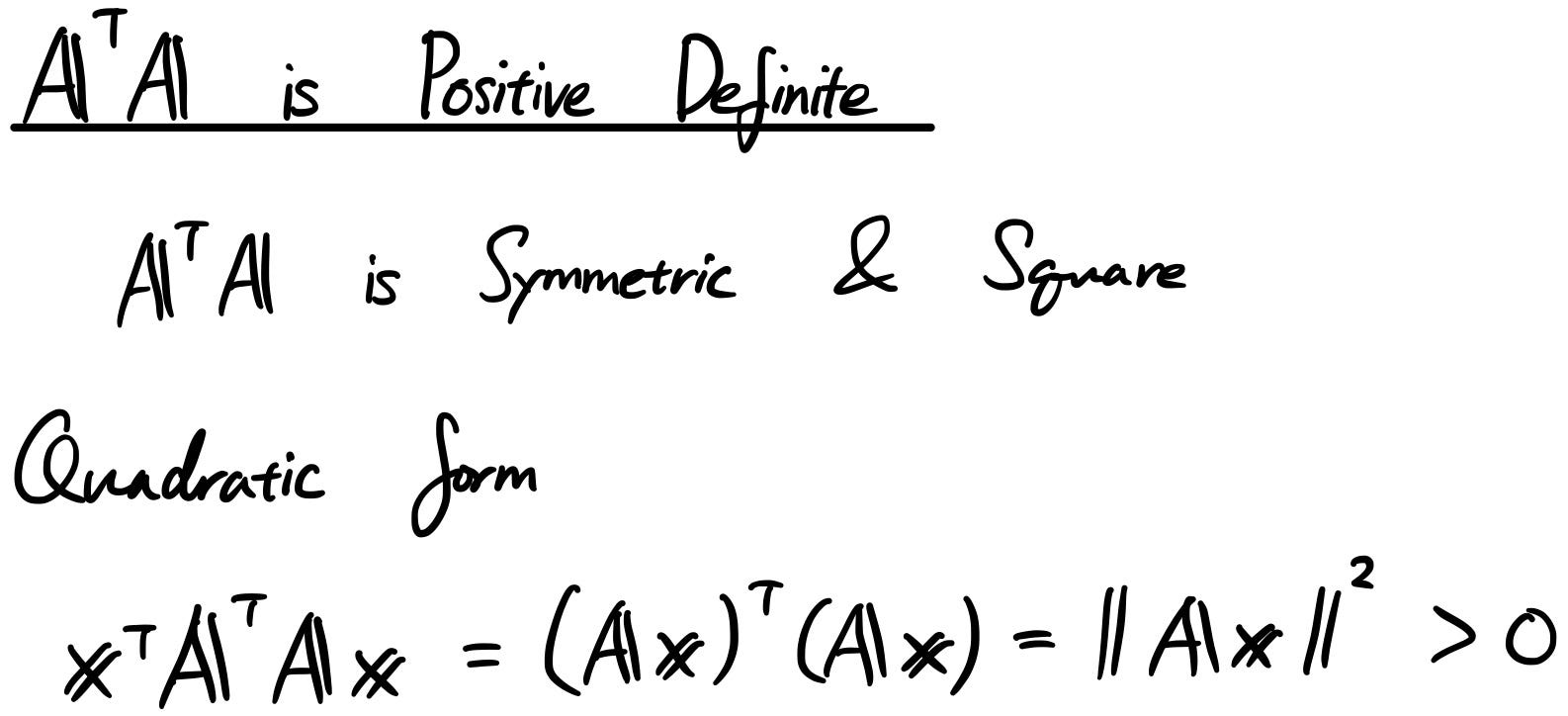
Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

Linear Algebra 101 Part 7 Eigendecomposition When Symmetric By Sho Nakagome Sho Jp Medium

Symmetric Matrices Eigenvalues Eigenvectors Youtube

Quadratic Forms And Positive Semidefinite Matrices Linear Algebra

Note Set 23a Totally For Sure Positive Definite Matrices Matrixology

Positive Definite Sequence And Its Corresponding Determinant Mathematics Stack Exchange

What Is A Positive Definite Matrix By Aerin Kim Towards Data Science

Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

Note Set 23a Totally For Sure Positive Definite Matrices Matrixology

Positive Definite Matrix

Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium

The Number Of Positive Eigenvalues Of A Non Singular Symmetric Matrix Is Equal To The Number Of Positive Pivots Strang Mathematics Stack Exchange

Test For Definiteness Of Matrix Ppt Video Online Download

Deducing That A Matrix Is Indefinite Using Only Its Leading Principal Minors Mathematics Stack Exchange

How To Check If A Matrix Is Positive Definite Quora

Prove That Determinant Of A 2x2 Symmetric Positive Definite Matrix Is Positive By Completing The Square Method Mathematics Stack Exchange

For A Symmetric Positive Definite Matrix Why Does Each Diagonal Element Exceeds The Small Eigenvalue Mathematics Stack Exchange