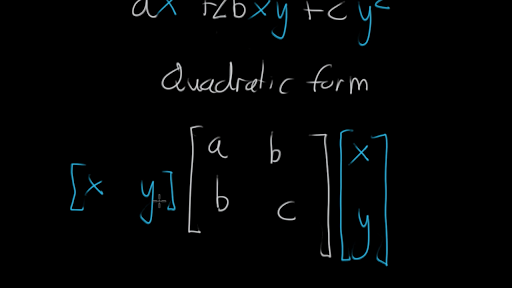Symmetric Matrix From Quadratic Form Calculator
It turns out that the matrix M is positive definite if and only if it is symmetric and its quadratic form is a strictly convex function I would be really surprised that symmetric is a necessary condition for positive definite. Indeed if aij 6 aji we replace them by new a0 ij a 0 ji aijaji 2 this does not change the corresponding quadratic form.

Express The Following Quadratic Form In The Matrix Chegg Com
Is Null Matrix 10.

Symmetric matrix from quadratic form calculator. For example the quadratic form 2 x26 xy -7y2can be written as where the coefficient 6 of the cross-product term has been split as 51 rather than 33 as in the symmetric representation. Is Identity Matrix 8. Eigen Value Matrix Calculator.
Free quadratic equation calculator - Solve quadratic equations using factoring complete the square and the quadratic formula step-by-step. LetQbe a quadratic form. Symmetric matrix Asymmetric matrixis a matrix A such that AT A.
The new basis is ñ. Quadratic Forms De nition 3. The function x 7kxkis a quadratic form given by setting A I.
This online calculator is a quadratic equation solver that will solve a second-order polynomial equation such as ax 2 bx c 0 for x where a 0 using the quadratic formula. Is Singular Matrix 14. Your first 5 questions are on us.
The calculator solution will show work using the quadratic formula. 12 Definiteness of Quadratic Forms. Symmetric Matrix Symmetric matrices are useful but not essential for representing quadratic forms.
A basis for R 3 of orthonormal eigenvectors of A q 1 X 2  2 Y 2  3 Z 2 In other words the new matrix for q wrt. Is Orothogonal Matrix 13. Quadratic form Suppose is a column vector in ℝ and is a symmetric matrix.
Suppose q is a quadratic form in variables xyz with matrix A. Thenx1for some symmetric matrixAxnExpanding this outQx1we see. Matrix Inverse determinant adjoint Eigen Value Eigen Vector Calculator.
14Note on symmetryThe matrix associated with a quadratic form B need not be symmetricHowever no loss of generality is obtained by assuming B is symmetric. Is Diagonal Matrix 7. Q1AQ QTAQ Λ hence we can express A as A QΛQT Xn i1 λiqiq T i in particular qi are both left and right eigenvectors Symmetric matrices quadratic forms matrix norm and SVD 153.
Auto Detect the matrix type 1. Such a matrix is necessarily square. Solve matrix equations step-by-step.
Ax 2 bx c 0. Symmetric Matrices and Quadratic Forms CSIE NCU 9 72 Quadratic forms A quadratic form on Rn is a function Q defined on Rn whose value at a vector x in Rn can be computed by an expression of the form Qx xTAx where A is an nxn symmetric matrix. Is Horizontal Matrix 5.
Is Column Matrix 3. Gexin Yu gyuwmedu Section 71 Diagonalization of symmetric matrices and 72 Quadratic forms. Get step-by-step solutions from expert tutors as fast as 15-30 minutes.
Watch the fir. The result of the quadratic form is a scalar. Parellelepiped Tetrahedron Volume Calculator.
Specificallyconsider a nonsymmetric matrix B and define A as 12B. There is an orthogonal Q st. Is Lower Triangle Matrix 11.
A quadratic form is a function Qon Rngiven by Qx xTAx where Ais an n n symmetric matrix called the matrix of the quadratic form. Is Row Matrix 2. Let A 5.
Show that the quadratic form of a matrix is 0 if and only if the matrix is skew symmetric ie show that q A x 0 for all x iff A t A. Is Square Matrix 4. Its main diagonal entries are arbitrary but its other entries occur in pairs on opposite sides of the main diagonal.
For example Enter a1 b8 and c16. Quadratic forms appear in di erential geometry physics economics and statistics. Is Scalar Matrix 9.
Conversely any polynomialof degree 2 can be written in this form. Generally one can find symmetrization A0 of a matrix A by A0 AAT 2. Is Vertical Matrix 6.
That xn x1xnA Qx1 xn XAijxixj 1ijn and so it is a polynomial with each term of degree 2. We can always take definiteand semidefinite matrices to be symmetric since they are defined by a quadratic form. In the section Quadratic forms it is said.
The term is called a quadratic form. Since A is symmetric it has a complete set of orthonormal eigenvectors with corresponding real eigenvalues  1 2 3. Is Upper Triangle Matrix 12.
Theorem 1 Any quadratic form can be represented by symmetric matrix.

Signature Of A Quadratic Form Mathoverflow

Symmetric Matrices Eigenvalues Eigenvectors Youtube

Express The Quadratic Form In The Matrix Notation X T Chegg Com

Write The Matrix Of Quadratic Form Youtube
Eigenvalues And Eigenvectors Of Symmetric Matrices Linear Algebra

Write The Matrix Of Quadratic Form Youtube

Consider The Quadratic Chegg Com

1 Find The Symmetric Matrix Of The Following Chegg Com
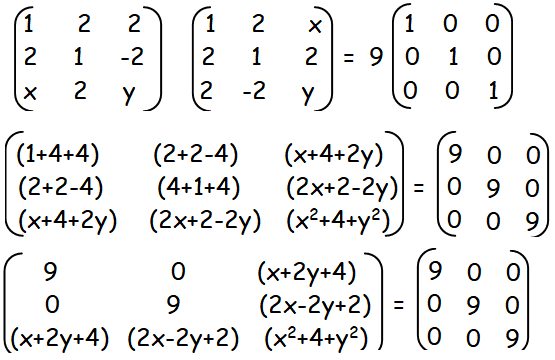
Example For Skew Symmetric Matrix
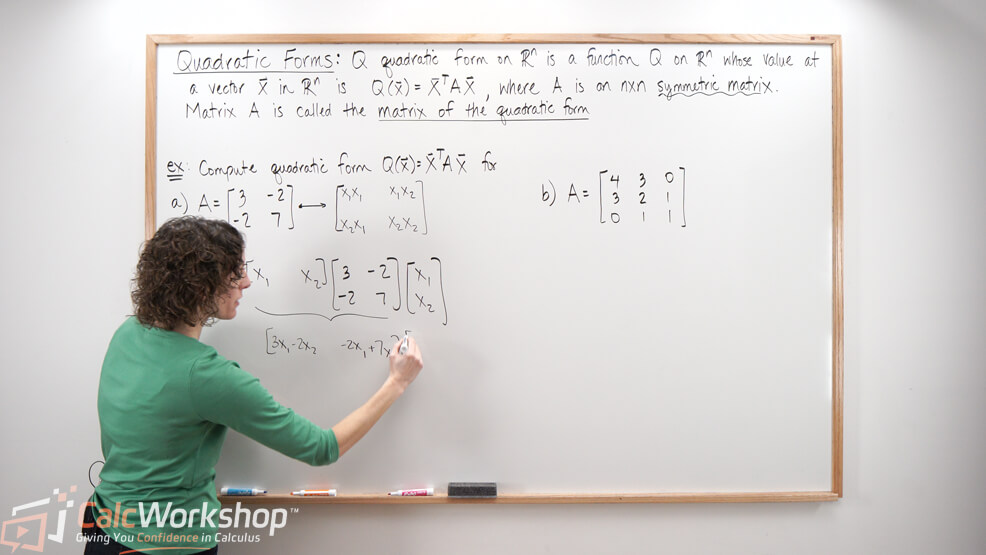
Matrix Of The Quadratic Form Calcworkshop

Quadratic Forms Characteristic Roots And Characteristic Vectors Ppt Video Online Download
Consider A Quadratic Form Q 3x1 3x2 3x3 Chegg Com

3 Consider The Following Quadratic Forms 9 X1 X2 Chegg Com

Expressing A Quadratic Form With A Matrix Youtube
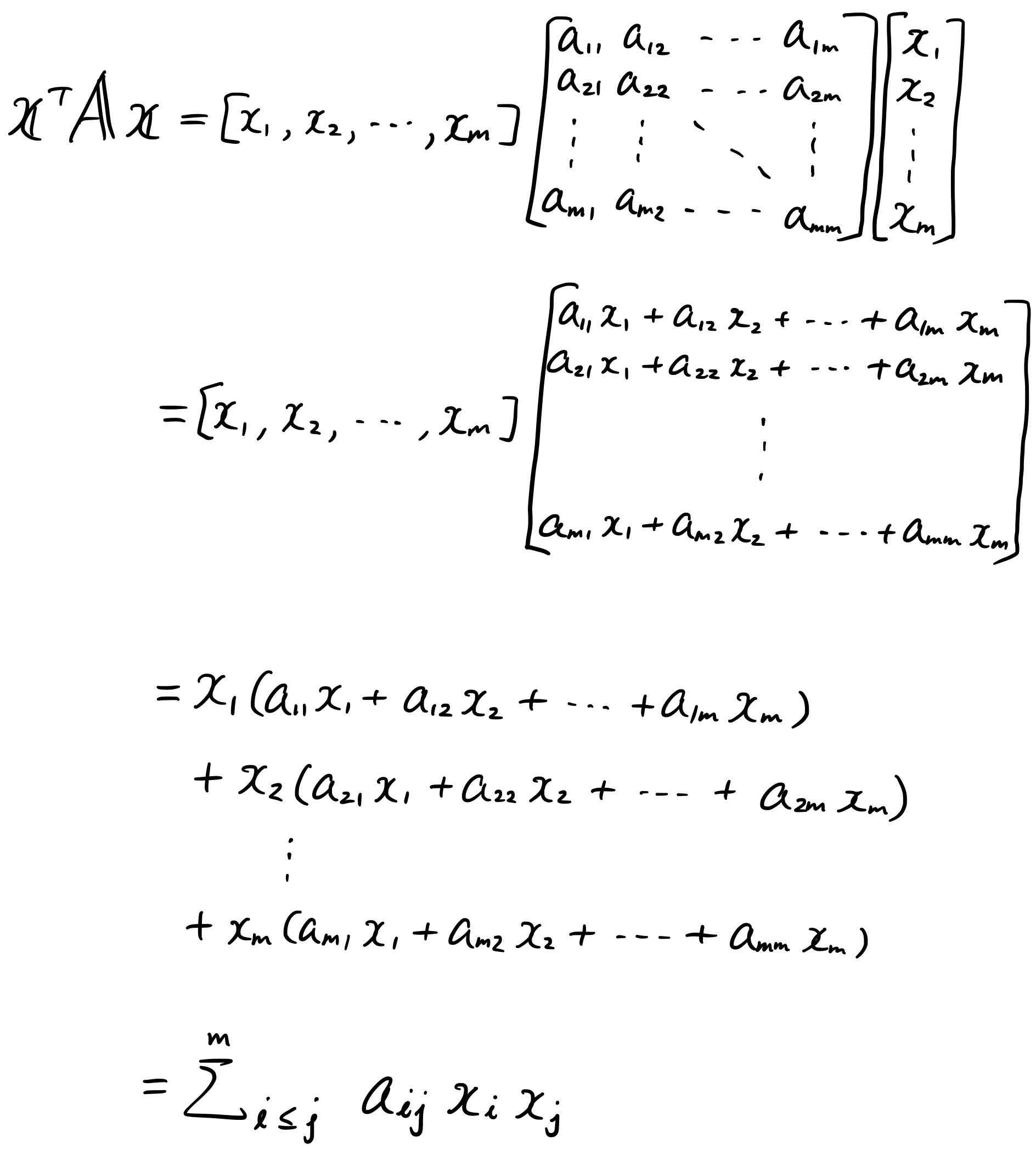
Linear Algebra 101 Part 8 Positive Definite Matrix By Sho Nakagome Sho Jp Medium
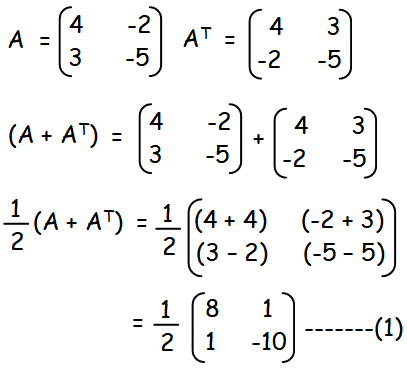
How To Express The Given Matrix As Sum Of Symmetric And Skew Symmetric
Algebraic Formulas And Matrix Symmetry Blog Bolner Hu
Expressing A Quadratic Form With A Matrix Video Khan Academy

Consider The Quadratic Form Q X Xỉ X2 X 4x1x2 Chegg Com