Calculate Determinant Of Covariance Matrix
Where xi is the i th row of the sample matrix. The Covariance Matrix is also known as dispersion matrix and variance-covariance matrix.

Construction Of The Joint Trait Phylogeny Covariance Matrix That Download Scientific Diagram
I would really appreciate if someone can help me figure this out.

Calculate determinant of covariance matrix. GMM GaussianMixture n_components2 covariance_typediag GMMfit X_train covariance_marix GMMcovariances_. The covariance between two jointly distributed real-valued random variables X and Y with finite second moments is defined as. For a 33 Matrix.
1 2 π Σ exp. To calculate a determinant you need to do the following steps. If they are random variables X a X b where a and b are constants.
Reduce this matrix to row echelon form using elementary row operations so that all the elements below diagonal are zero. Free matrix determinant calculator - calculate matrix determinant step-by-step This website uses cookies to ensure you get the best experience. 1 2 ϵ Σ 2 What I want to know is why do we use the determinant of the covariance matrix in the multivariate case.
F x displaystyle f x so that it integrates to 1. Here the covariance matrix is not asquare. The covariance matrix Σ is the multidimensional analog of what in one dimension would be the variance and.
To work out the determinant of a 33 matrix. I need calculate the determinant of a covariance matrix of a multivariate normal distribution I want to know is there any rapid way or code for this purpose thanks for your help. Det C detL det L detL detL But the determinant of a lower triangular matrix is the product of its diagonal elements so taking logs above we.
B 1 1. By using this website you agree to our Cookie Policy. 1 2 ϵ σ 2 and as follows for the multivariate case.
Σ-1 is the d d SPD precision matrix. This code however seems timing complexity and run pretty slow especially when handling a larger matrix for instance 1000times1000 matrix. The matrix B1_j is obtained by deleting row 1 and column j from the matrix mathbfB.
By definition the generalized variance of a random vector mathbfX is equal to sum the determinant of the variancecovariance matrix. Symmetry means that the matrix and its transpose are identical ie bf A bf A. A covariance matrix with zero determinant means that the random variables are perfectly correlated.
H p k 2 1 ln. On the other hand this matrix B has a determinant value very far from 0 but is horribly conditioned. The differential entropy of a Gaussian density is defined as.
A aei fh bdi fg cdh eg The determinant of A equals. That is X c 0 almost surely and your equation follows where we defined X X E X. If you compute the determinant of the sample covariance matrix then you measure indirectly the differential entropy of the distribution up to constant factors and a logarithm.
If your X and X are vectors one is an affine function of the other. If not for the scaling factor of 1eps the determinant would suggest its very close to singular which the condition number supports but the scaling factor inflates the determinant value. If you perform a cholesky factorisation of the covariance C with lower triangular factor L say so that.
For a 33 matrix 3 rows and 3 columns. The covariance matrix VX of X is defined to be the symmetric n by n matrix with entries v ij. E X X c 0 in particular c E X X c 0 E X c 2 0 X c 2 0 almost surely.
Determinant of Σ Σ is the d d SPD covariance matrix. 1 i j n given by Vij COVX i X j. Multiply the main diagonal elements of the matrix - determinant is calculated.
Determinant of variance-covariance matrix Of great interest in statistics is the determinant of a square symmetric matrix bf D whose diagonal elements are sample variances and whose off-diagonal elements are sample covariances. Multiply a by the determinant of the 22 matrix that is not in as row or column. Set the matrix must be square.
See eg Multivariate normal distribution. C LL then. Input the matrix in the text field below in the same format as matrices given in the examples.
Det E X X 0 c R N. 2 π p 2 det Σ 1 2 displaystyle 2pi - frac p 2det Sigma - frac 1 2 normalizes the density. Etc It may look complicated but there is a pattern.
In the univariate case we have the variance sigma2 but in the multivariate case we write the determinant of the variance. Button and find out the covariance matrix of a multivariate sample. The covariance matrix VX of X is.
X n be a vector of random variables. Where N Number of scores in each. Write f x n q x where q x x-μ Σ-1 x-μ R R exponential R d R quadratic Now q x is a function we understandits just a quadratic bowl centered at μ the quadratic form of the precision matrix.
X A X B where A is some matrix and B a vector. 1 2 π σ 2 exp. Let X X 1 X 2.
The covariance matrix of any sample matrix can be expressed in the following way. The generalized variance can be estimated by calculating S the determinant of the sample variancecovariance matrix.

3 28 The Trace And The Determinant Of A Covariance Matrix Youtube

Making A Covariance Matrix In R Stats Seandolinar Com

Why Does This Covariance Matrix Have A Rank Of N Cross Validated

How Is The Determinant Of X X Related To Variance Cross Validated
What Is The Physical Meaning Of Inverse Covariance Matrix Or Concentration Matrix Or Precision Matrix And How Does One Calculate It Quora
Risk Part 3 Variance Covariance Matrix Varsity By Zerodha

Statistics 101 The Covariance Matrix Youtube

How To Derive Variance Covariance Matrix Of Coefficients In Linear Regression Cross Validated
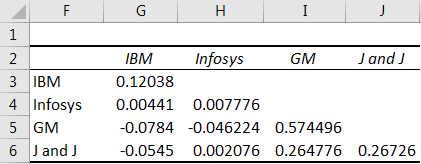
Covariance Matrix In Excel Step By Step Guide With Examples
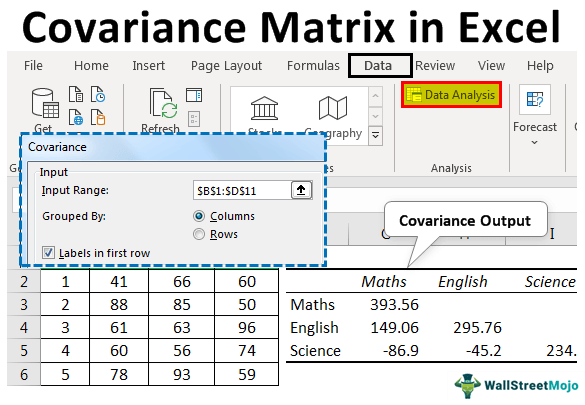
Covariance Matrix In Excel Step By Step Guide With Examples

A Covariance Matrix For Three Traits A B And C The Diagonal Download Scientific Diagram
How Do I Enter A Sample Covariance Matrix
Xleratordb Math Documentation Sql Server Covariance Matrix Function
Risk Part 3 Variance Covariance Matrix Varsity By Zerodha
Risk Part 3 Variance Covariance Matrix Varsity By Zerodha

Bivariate Normal Distribution Matrix Approach Youtube
Risk Part 3 Variance Covariance Matrix Varsity By Zerodha
The Determinant Of The Covariance Matrix Is 0 1 Determinant For Exams Programmer Sought

Covariate Assisted Principal Regression For Covariance Matrix Outcomes Biorxiv
