Matrix Product Index Notation
Make the inner index k in this case the same and sum over it Example. Conventions and special symbols for index notation Range Convention.

Cross Products Using Levi Civita Symbol Youtube
Is also know as a Kronecker product is defined in terms of the index notation by writing 26 b lje j la kie i k b lja kie ji lk.
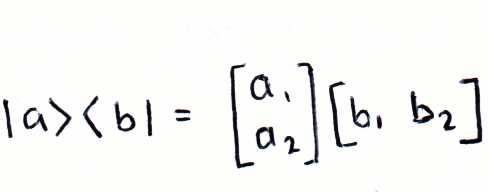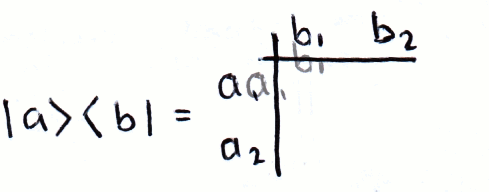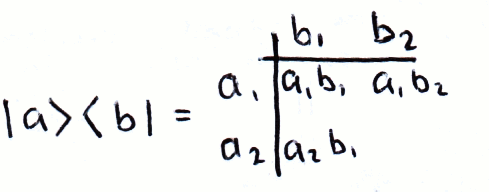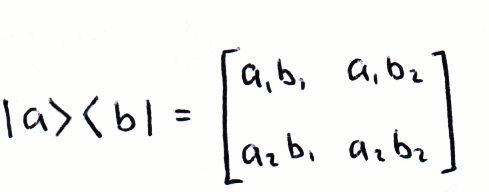
Matrix product index notation. V and index notation. The symbol Sij denotes nine components of a second order tensor S11 S12 S13 S21. Matrix notation is well suited for two-way data such as measurements of many objects on multiple variables and for two-way models such as the structure given by a product of two or three matrices.
The index notation for these equations is. Recall that given any two matrices A Aij and B Bij the matrix product is a new matrix AB Cij defined as follows. It also indicates that the the second dimension of the matrix must match that of the vector.
For instance to indicate the sum of the diagonal elements of the stress matrix we can write. 41 Vector Product in index notation Recall ab i j k ax ay az bx by bz Now consider ci εijkajbk This is a vector characterized by a single free index i. I i j ij b a x ρ σ 7111 Note the dummy index.
The trace of a matrix is de ned to be the sum of its diagonal elements TrC X i C ii 12 We would like to prove that TrAB TrBA 13 2. As part of mathematics it is a notational subset of Ricci calculus. However it is often used in applications in physics that do not.
Consider the vectorsa andb which can be expressed using index notation as a a 1ˆe 1 a 2ˆe 2 a 3eˆ 3 a iˆe i b b 1ˆe 1 b 2ˆe 2 b 3eˆ 3 b jˆe j 9 Note that we use different indices i and j for the two vectors to indicate that the index forb is completely independent of that used fora. Begineqnarray C BA C_ij mathop _k12B_ ikA_kjquad text B_ikA_kj in the summation convention 531 endeqnarray. For the matrix-vector case there are several things made apparent by the indicial no-tation.
The rule for matrix multiplication is. For instance to indicate the sum of the diagonal elements of the stress matrix. 3 σ kk σ kk σ11 σ22 σ33 k1 The multiplication rule for matrices can be stated formally by taking A a ijtobean MNmatrixandBb ijtobeanR P matrix.
I or simply. Matrix 2nd order tensor A ij A ij If A 2 4 a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 3 5then A 23 a 23 Kronecker delta 2nd order tensor ij I ij ˆ 1 if i j 0 if i6 j To indicate operation among tensor we will use Einstein summation convention summation over repeated indices u iu i X3 i1 u iu i iis called dummy index as opposed to free index and can be renamed. The abstract way to write a matrix multiplication with indices.
By breaking down to each individual operation of multiplicationtransposition it is easier. The index i is called a j free index. The matrix product AB is defined.
So in a matrix indexed by i and j the diagonal components equal 1and the off-diagonal components equal 0. Here eji lk stands for a matrix of order st mn with a unit in the row indexed by lkthe l 1skth rowand in the column indexed by jithe j 1mith columnand with zeros elsewhere. Or dot products using index notation.
IjtobeanRPmatrixThematrixproductAB isde ned onlywhenRNandistheMPmatrixCc ijgivenby c ij XN k1 a ikb kj a i1b1j a i2b2j a iNb Nk Usingthesummationconventionthiscanbewrittensimply c ij a ikb kj wherethesummationisunderstoodtobeovertherepeatedindexkInthecaseofa33 matrixmultiplyinga3 1columnvectorwehave 2 6 4 a11 a12 a13 a21 a22 a23 a31 a32 a33 3 7 5 8. D Ab 9 d i A ijb j 10 The repeated index j indicates that you should sum over the index j this is illustrated in detail below. Use new names to keep track of everything to avoid confusion.
712 Matrix Notation. A subscript that is repeated in a given term is understood to imply summation over the range of the repeated subscript. Define D B T and E A D that way you want the i j th entry of F E C.
B1 b2 b3 9. Lower case Latin subscripts i j k have the range 1 2 3. If one term has a free index i then to be consistent all terms must have it.
One free index as here indicates three separate equations. D l m b m l e n o a n p d p o a n p b o p f i j e i k c k j a i p b k p c k j. This is the summation convention for index notation.
This is the summation convention for index notation. In index notation a vector u is represented as u i a two-dimensional matrix A is represented as A ij and an N-dimensional matrix B is represented as B ij m where the number of subscripts i through m is equal to NThe same index may not appear more than twice in. The indices j and k are dummy indices and are summed out.
The symbol xi denotes three components of a vector x1 x2 and x3. Cij AikBkj In particular if we think of the first index as the row index and the second index as the column index then we see that in the matrix product the column index of the first matrix factor matrix A is being summed with the row index of the second factor matrix B. The Kronecker Delta delta_ij serves as the identity matrix bf I because it equals 1 when i j and 0 otherwise.
We get the three values of ci by letting i 123 independently. In mathematics especially in applications of linear algebra to physics the Einstein notation or Einstein summation convention is a notational convention that implies summation over a set of indexed terms in a formula thus achieving notational brevity. Of the repeated subscript.
The symbolic notation. Trace of a product of matrices.
Applied Mechanics Of Solids A F Bower Appendix C Index Notation
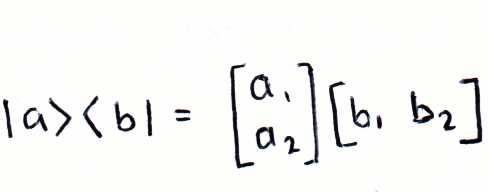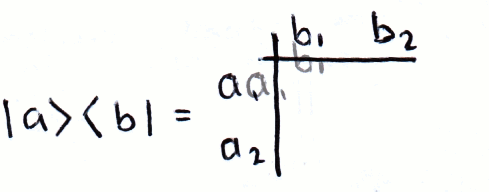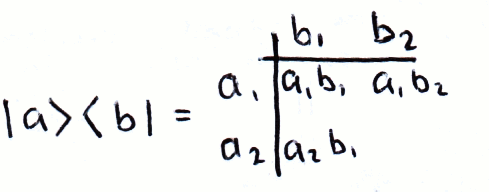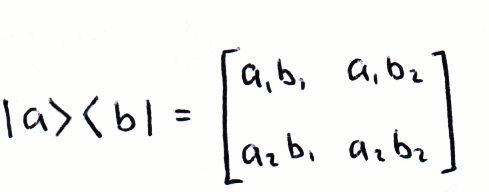
Dirac Notation Basic Matrix Algerbra Cnot

Matrix Multiplication Refer To This Video By Mathispower4u By Solomon Xie Linear Algebra Basics Medium

Kronecker Matrix Product Properties Youtube

Limits How To Solve Basic Limits Problems Solved Example 1 Problem Solved Solving Calculus
Applied Mechanics Of Solids A F Bower Appendix C Index Notation

Dot Product Explained Basic Physics Physics 12th Maths
Applied Mechanics Of Solids A F Bower Appendix C Index Notation

How Do I Represent A Transpose A In Indicial Notation Physics Stack Exchange
Applied Mechanics Of Solids A F Bower Appendix C Index Notation

How To Multiply Two Matrices Together Studypug

Linear Algebra 07 Index Notation Youtube
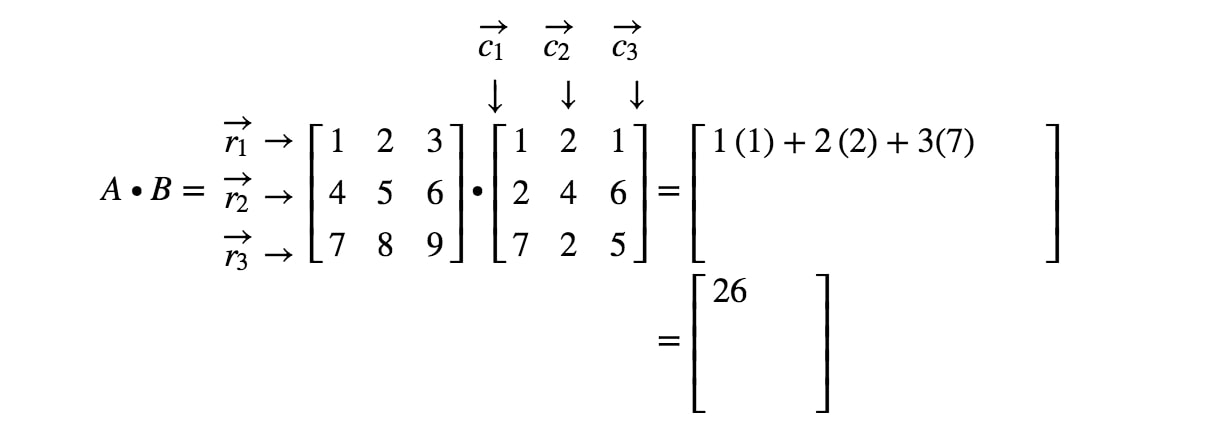
How To Multiply Two Matrices Together Studypug
Bme 456 Mathematical Preliminaries
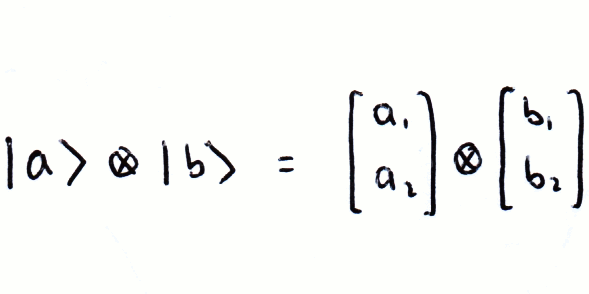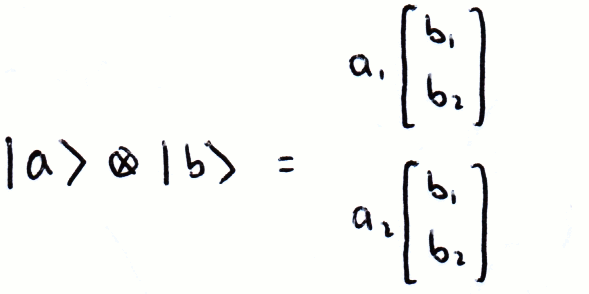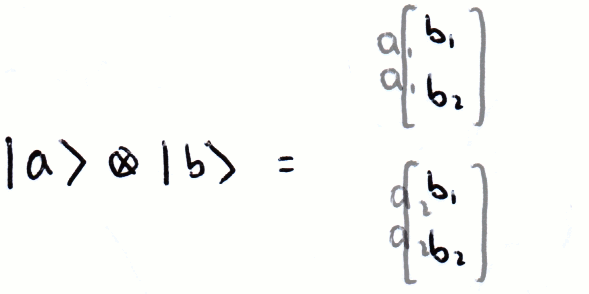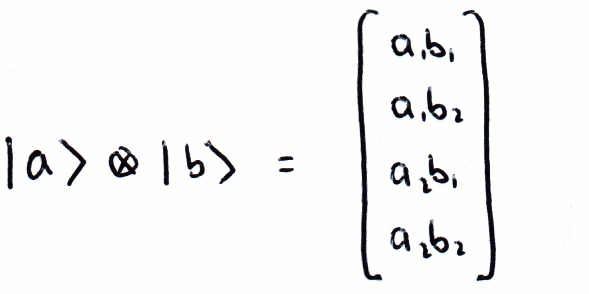
Dirac Notation Basic Matrix Algerbra Cnot
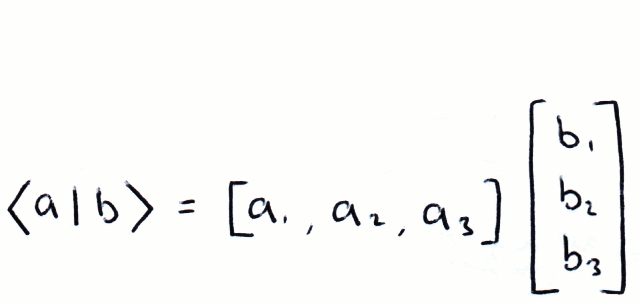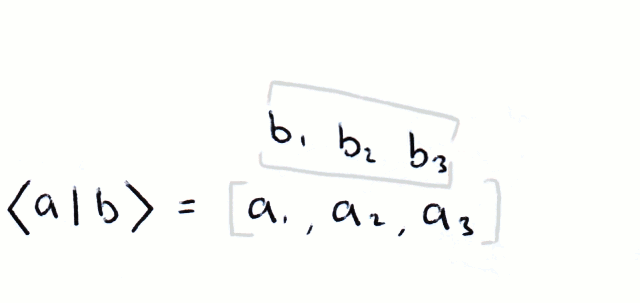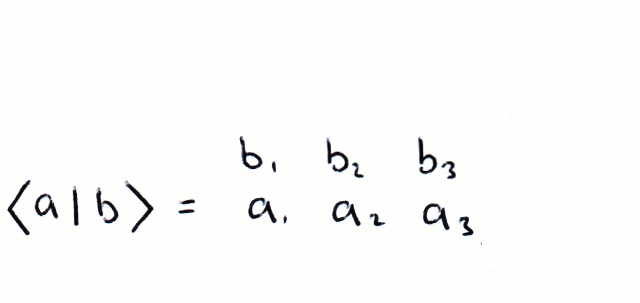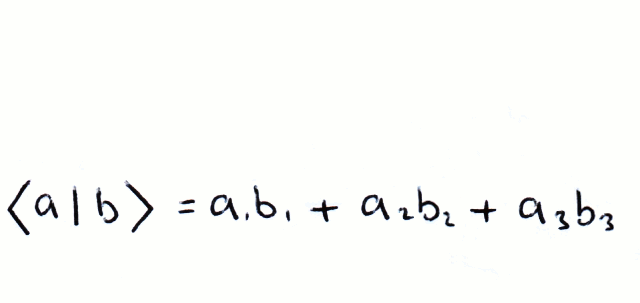
Dirac Notation Basic Matrix Algerbra Cnot


