Singular Matrix Dimensionality Reduction
Xk1 Mxk kMxkk where kNk for a matrix or vector N denotes the Frobenius norm. Regardless of how many singular values you approximately set to zero the resulting matrix A always retains its original dimension.
Understanding The Mathematics Behind Principal Component Analysis By Nikita Sharma Heartbeat
Let M be the matrix whose eigenpairs we would like to find.

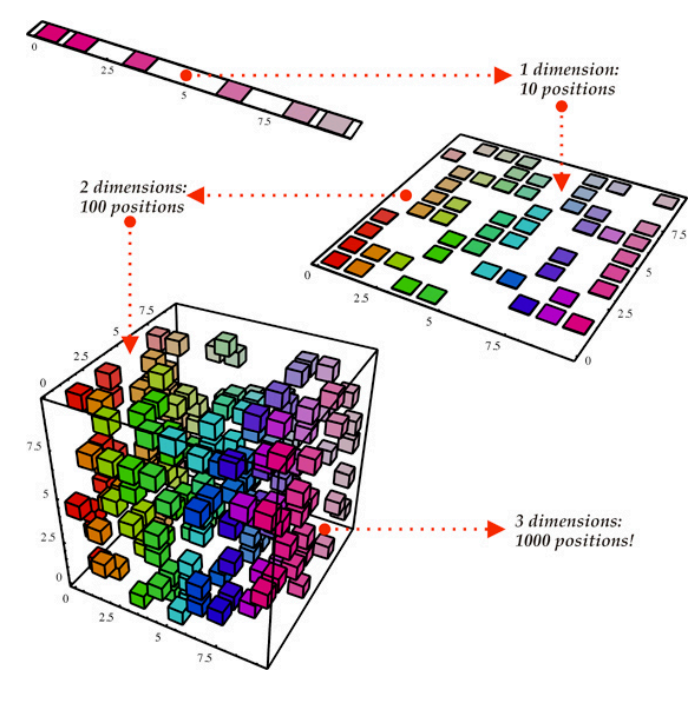
Singular matrix dimensionality reduction. A UV where. Dimensionality reduction is the process of reducing the number of variables under consideration. SVD can be used for dimensionality reduction of large genomic datasets.
For the case of simplicity we will focus on the SVD for real-valued matrices and ignore the case for complex numbers. Singular value decomposition SVD. SVD decomposes a matrix into three other matrices.
Using SVD the dimensionality of data can be reduced by projecting data onto the space spanned by the left singular vectors corresponding to the k largest singular values given by Where U_k is of size d k and contains k singular vectors. That is the square root of the sum of the squares of the elements of N. It can be used to extract latent features from raw and noisy features or compress data while maintaining the structure.
Matrix data have some special statistical methods that can be applied to them. Singular Value Decomposition SVD is used to simplify the values within a matrix reducing the matrix down to its constituent parts and making calculations with that matrix easier. The Singular-Value Decomposition or SVD for short is a matrix decomposition method for reducing a matrix to its constituent parts in order to make certain subsequent matrix calculations simpler.
Singular Value Decomposition SVD is one of the widely used methods for dimensionality reduction. In particular you dont drop any rows or columns. Singular value decomposition SVD Singular value decomposition SVD factorizes a matrix into three matrices.
Like PCA SVD is also expensive to compute. Dimensionality reduction refers to reducing the number of input variables for a dataset. SVD decomposes a mxn real matrix A into a product of three matrices in the form.
Singular Value Decomposition for Dimensionality Reduction by Niranjan B Subramanian Singular Value Decomposition usually referred to as SVD is a type of matrix decomposition technique that is popularly used to reduce the dimensions of the data. Start with any nonzero vector x0 and then iterate. Now dimensionality reduction is done by neglecting small singular values in the diagonal matrix S.
U Sigma and V such that A U Sigma VT where U is an orthonormal matrix whose columns are called left singular vectors. SVD can be utilized for both real-value and complex matrices but for the purposes of this explanation will examine how to decompose a matrix of real values. Sparkmllib provides support for dimensionality reduction on the RowMatrix class.
If we see matrices as something that causes a linear transformation in the space then with Singular Value Decomposition we decompose a single transformation in three movements. Singular Value Decomposition SVD is a dimensionality reduction technique similar to PCA but more effective than PCA. In the first step SVFS uses the signature matrix S_D of D to find the cluster that contains mathbf b.
SVD or Singular Value Decomposition is one of several techniques that can be used to reduce the dimensionality ie the number of columns of a data set. We multiply the current vector xk by the matrix M until convergence ie kxk xk1k is less. If your data is represented using rows and columns such as in a spreadsheet then the input variables are the columns that are fed as input to a model to predict the.
So just like PCA we only keep number of singular. Sparkmllib provides support for dimensionality reduction on the RowMatrix class. It is considered as factorization of a data matrix into three matrices.
Matrix S is a diagonal matrix with singular values sorted in decreasing order so as you use more singular values matrix will look closer to A. In predictive analytics more columns normally means more time required to build models and score data. After SVD genomic prediction using dense genomic data and many genotyped individuals can.
We reduce the size of A by discarding features in the other clusters as. One category of statistical dimension reduction techniques is commonly called principal components analysis PCA or the singular value decomposition SVD. Why would we want to reduce the number of dimensions.
The diagonal matrix S contains the singular values of X. Given a rectangular matrix A which is an n x p matrix the SVD theorem shows that this matrix can be represented as.
Dimension Reduction Motivation

Chapter 9 Dimensionality Reduction Orchestrating Single Cell Analysis With Bioconductor

Lecture 48 Dimensionality Reduction With Svd Stanford University Youtube

Dimensionality Reduction Techniques Python

Tensor Decomposition For Dimension Reduction Cheng 2020 Wires Computational Statistics Wiley Online Library
Dimensionality Reduction How To Deal With The Features In Your Dataset Part 1 By Anuradha Das Analytics Vidhya Medium
Does Dimension Reduction Always Lose Some Information Cross Validated
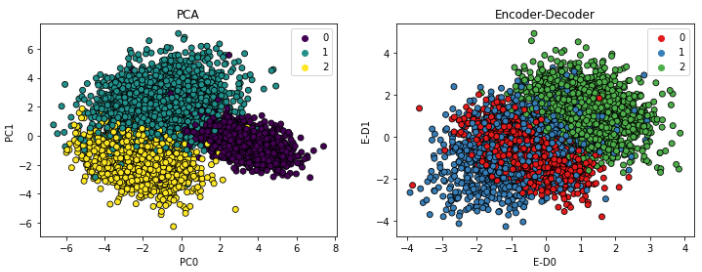
Dimensionality Reduction Towards Data Science
Using Svd For Dimensionality Reduction Oracle R Technologies Blog

Unpacking Pca A Practical Implementation Of By Ryota Bannai Towards Data Science

Dimensionality Reduction An Overview Sciencedirect Topics

Machine Learning For Humans Part 3 Unsupervised Learning Machine Learning Principal Component Analysis Dimensionality Reduction

Ai Singular Value Decomposition For Dimensionality Reduction In Python Ai A I Reducing The Dimensionality Reduction Making Predictions Recommender System

Dimensionality Reduction Techniques Python
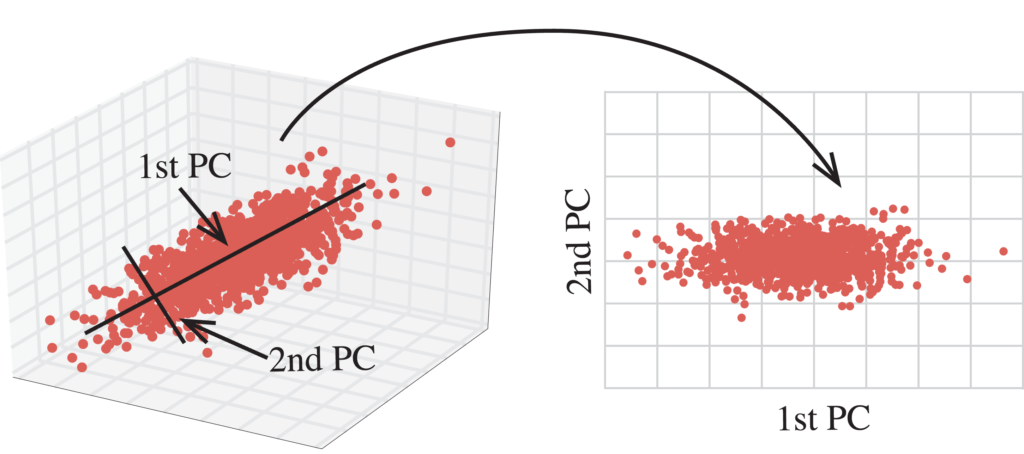
Day 10 Dimensionality Reduction With Pca And T Sne In R By Saigayatri Vadali Medium

Pca And Svd Explained With Numpy How Exactly Are Principal Component By Zichen Wang Towards Data Science
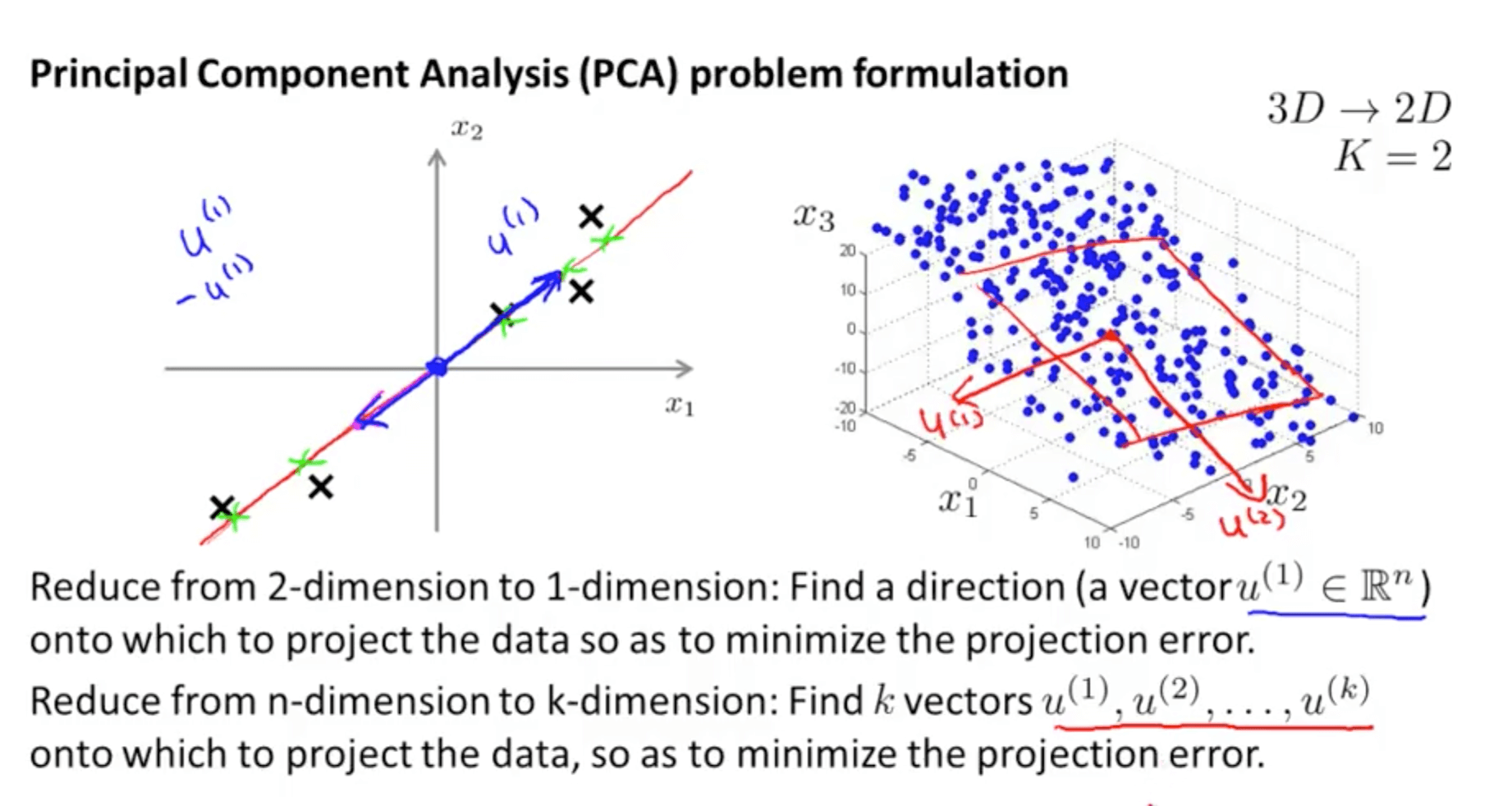
Dimensionality Reduction Machine Learning Deep Learning And Computer Vision

Sklearn Pca Svd Dimensionality Reduction Youtube
