Matrix Matrix Multiplication Complexity
But there are faster algorithms for particular types of matrices -- if you know more you may be able to do better. Complexity of matrix multiplication is.

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
The first algorithm diagonalizes your matrix which is usually possible writing it as M P D P 1 where M D in general may be complex-valued.
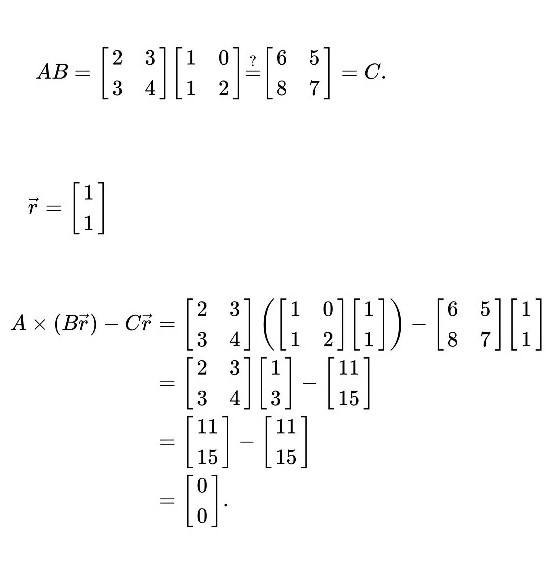
Matrix matrix multiplication complexity. The main condition of matrix multiplication is that the number of columns of the 1st matrix must equal to the number of rows of the 2nd one. There are specifically adapted algorithms for say solving linear systems ax b for sparse matrices a such as the conjugate. That the inner dimensions of pSrcA and pSrcB are equal.
No of columns in the first matrix should be equal to the number of rows of the second matrix. A BC AB C It is not commutative ie A BC not equal to A C B To multiply two matrices they should be compatible ie. ω 11k inf 𝜏𝜏this product can be computed using arithmetic operations.
A matrix is a rectangular array of numbers or other mathematical objects for which operations such as addition and multiplication are defined. The best known algorithm has complexity approximately On23728639. Exponent of Rectangular Matrix Multiplication.
Further if the matrix A is arbitrary one would need mn time see Exercise 13. Most of this article focuses on real and complex matrices that is matrices whose elements are respectively real numbers or complex. Where A MxN complex vakued matrix C NxN complex vakued matrix and RNxN real valued matrix.
In particular matrix multiplication the main concepts in low degree algebraic complexity theory have been introduced for the study of the complexity of matrix multiplication Algebraic complexity theory. Complex Matrix multiplication is only defined if the number of columns of the first matrix equals the number of rows of the second matrix. Stands for Hermitian transpose.
Bentuk matriks axb dan xab adalah salah satunya materi matriks yang terbilang mudah. Assuming that each operation for an field F can be done in O1 time this implies that the worst-case complexity of matrix-vector multiplication is mn. X stands for matrix multiplication.
Nur Dean The Graduate Center Matrix Multiplication 05012017 8 36. Complex matrix multiplication MATLAB. And then multiplying this M P matrix by C requires multiplying and adding P terms for each of M N entries.
Compute the product of an. So far I am doing this operation using npdot.
2 hours agoand want to compute npdotan where n is a covariance matrix that has entries everywhere symmetric and positive definite. However it is unknown what the underlying complexity actually is. For example if you multiply a matrix of n x k by k x m size youll get a new one of n x m dimension.
Do you have recommendations how to speed it up using either npeinsum or to exploit the block diagonality of matrix a. The complete solution to axb. Please suggest which of follwing will have higher computaional complexity.
Exponent of rectangular matrix multiplication. When matrix size checking is enabled the functions check. Ax b a11 a 21.
Multiplication however has a time complexity of O xn ym where x m is number of columns and terms in the second matrix. See the wikipedia article on matrix multiplication. As a result of multiplication you will get a new matrix that has the same quantity of rows as the 1st one has and the same quantity of columns as the 2nd one.
So the total complexity is. Matrix multiplication is associative ie. The naive algorithm has complexity Omjn for multiplying an m x j matrix by a j x n matrix or On3 for square n x n matrices.
So the complexity is O N M P. If all of those are n to you its O n3 not O n2. It will not be O n2 in the general case.
Most commonly a matrix over a field F is a rectangular array of scalars each of which is a member of F. Here you can perform matrix multiplication with complex numbers online for free. And y n is number of rows and terms in the first matrix.
Study of computation using algebraic models. Note its very easy to raise a diagonal matrix to the n th power. Exponent of rectangular matrix multiplication.
The naive matrix multiplication for A B involves multiplying and adding N terms for each of M P entries in A B. T 1 n22n 1 where is the execution time for an elementary computational operation such as multiplication or addition. Multiplying an M x N matrix with an N x P matrix results in an M x P matrix.
The standard way of multiplying an m-by-n matrix by an n-by-p matrix has complexity O mnp. You then compute M P D n P 1.

Communication Costs Of Strassen S Matrix Multiplication February 2014 Communications Of The Acm

Time Complexity Of Some Matrix Multiplication Mathematics Stack Exchange
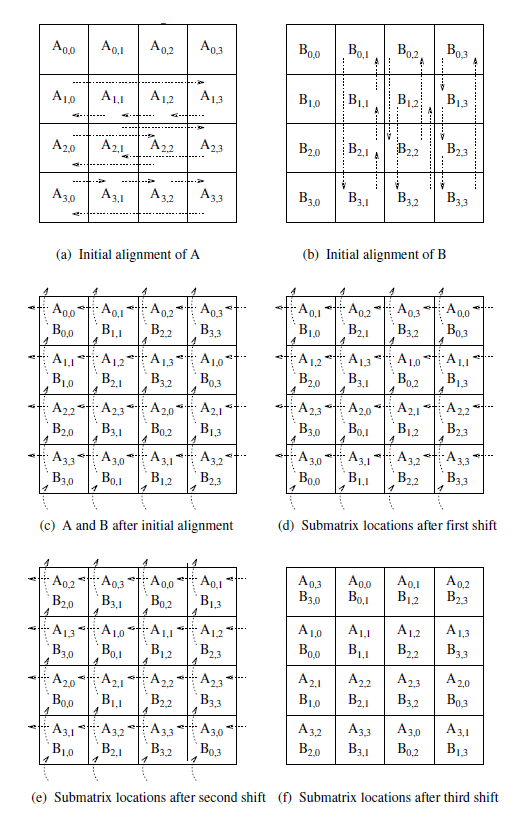
Cannon S Algorithm For Distributed Matrix Multiplication
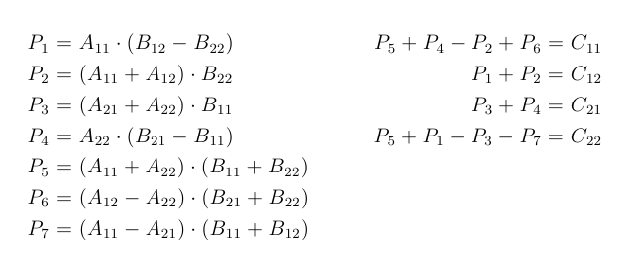
Strassen Matrix Multiplication C The Startup

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov

Matrix Chain Multiplication Dynamic Programming Youtube
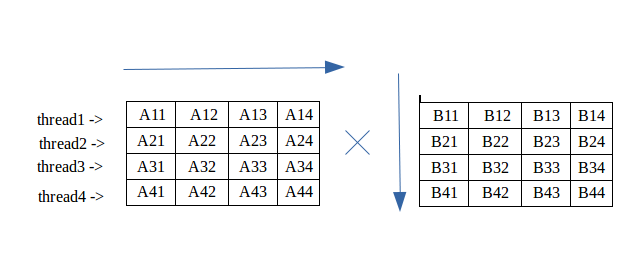
Multiplication Of Matrix Using Threads Geeksforgeeks

Toward An Optimal Matrix Multiplication Algorithm Kilichbek Haydarov
Cannon S Algorithm For Distributed Matrix Multiplication

Tuning Strassen S Matrix Multiplication For Memory Efficiency

Strassen S Matrix Multiplication Divide And Conquer Geeksforgeeks Youtube

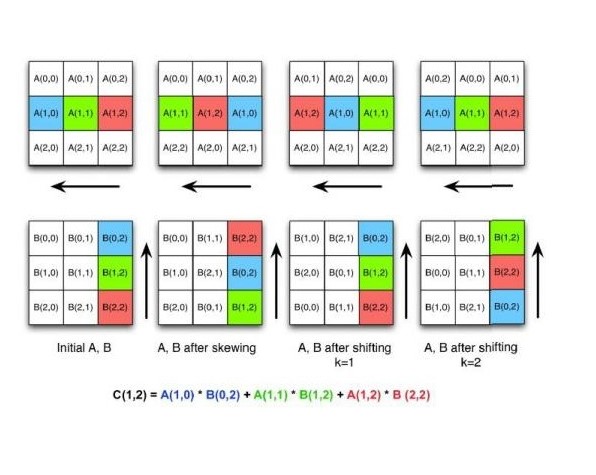
Systolic Arrays Algorithm For Matrix Multiplication Mathematics Stack Exchange

Strassen S Matrix Multiplication Algorithm When N Is Not A Power Of 2 Computer Science Stack Exchange
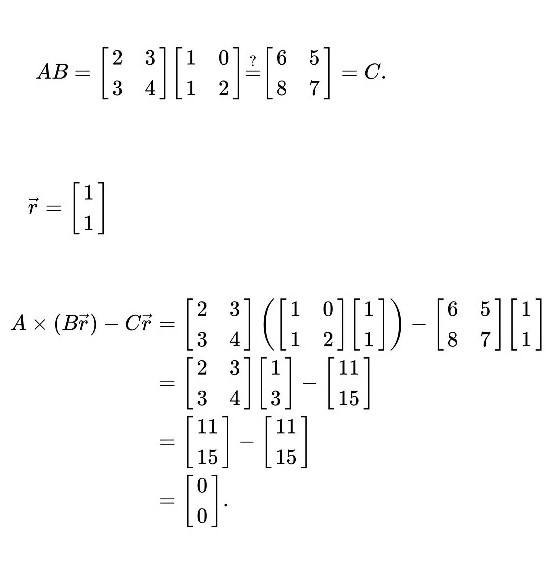
Freivalds Algorithm For Verifying Matrix Multiplication

2 9 Strassens Matrix Multiplication Youtube
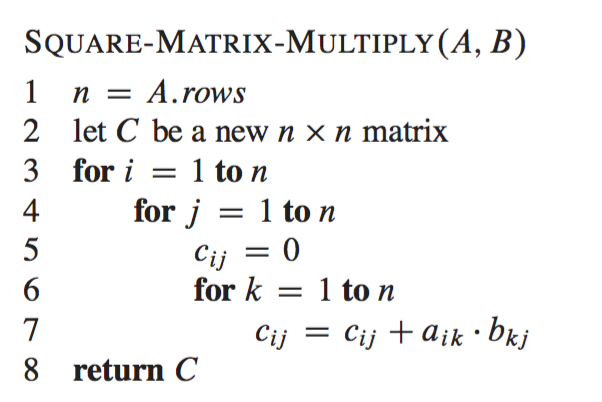
Matrix Multiplication Using The Divide And Conquer Paradigm
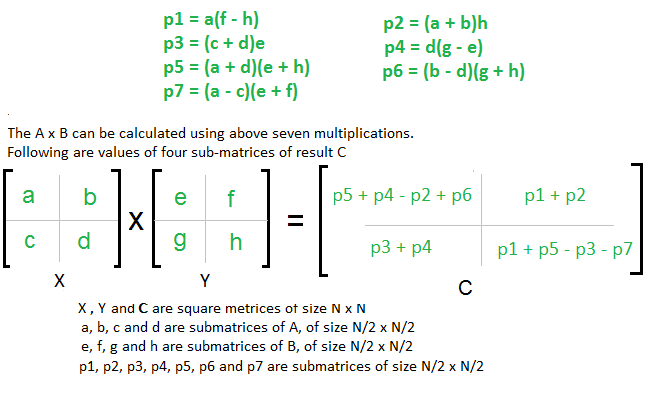
Easy Way To Remember Strassen S Matrix Equation Geeksforgeeks
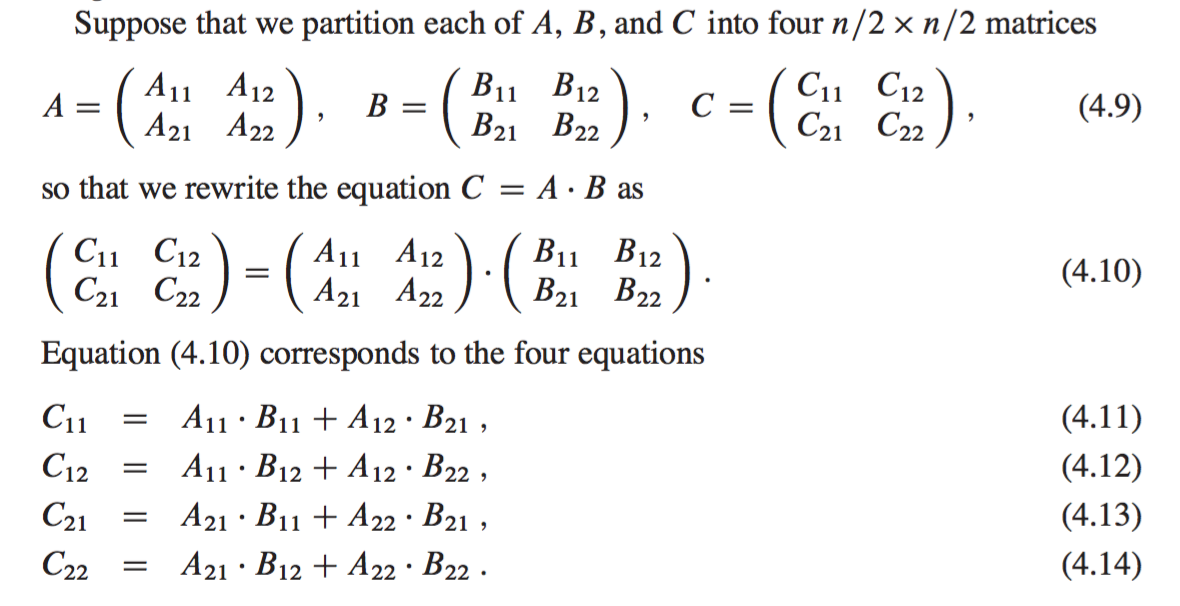
Matrix Multiplication Using The Divide And Conquer Paradigm