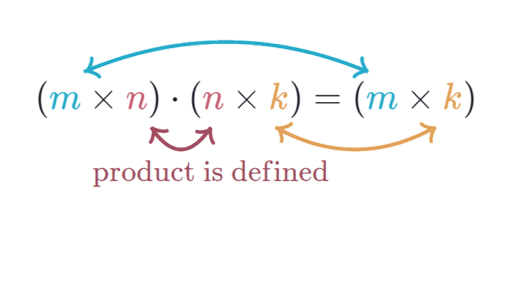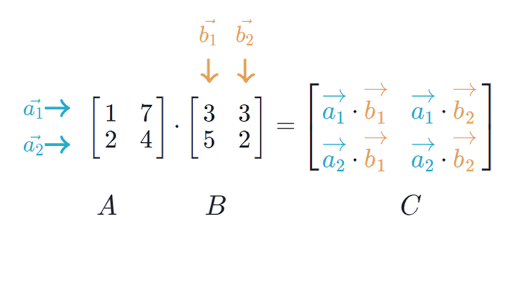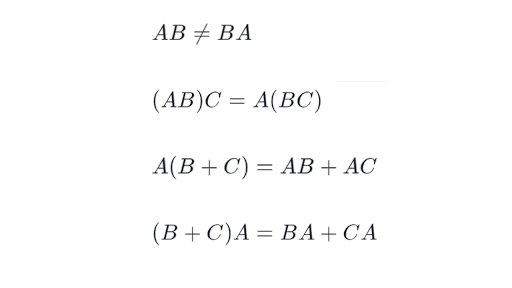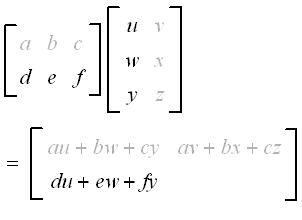Matrix Multiplication And Transpose Rules
Transpose matrix means moving position of the elements. Let A a ij and B b ij of size m n.
Matrix Multiplication Dimensions Article Khan Academy
I is the identity matrix and R is a real number.

Matrix multiplication and transpose rules. KA B kA kB Distributivity of scalar multiplication II 3. Let us consider A B and C are three different square matrices. AB BA Commutative Law of Addition.
K A kA A Distributivity of scalar multiplication I 2. αβA αβA αABαAαB. The transpose of matrix A is determined as shown below.
6 7 m1 AB m2 B. If a matrix is multiplied by a constant and its transpose is taken then the matrix obtained is equal to transpose of original matrix multiplied by that constant. ABC ABACDistributivity of matrix multiplication 4.
The algebra of matrix follows some rules for addition and multiplication. It has symbol T in top right-hand corner of the matrixs name. Now as per the rules of laws of matrices.
Definition The transpose of an m x n matrix A is the n x m matrix AT obtained by interchanging rows and columns of A Definition A square matrix A is symmetric if AT A. A Tb b a the result is a scalar and the transpose of a scalar is itself A BC AC BC multiplication is distributive a b T C a T C b T C as above with vectors. First multiply all elements of the i th row of the matrix A pairwise with all the elements of the j th column of the matrix B.
Transpose of Addition of Matrices. The transpose of an m nmatrix Ais the n mmatrix AT whose columns are the rows of A. ABTATBT the transpose of a sum is the sum of transposes.
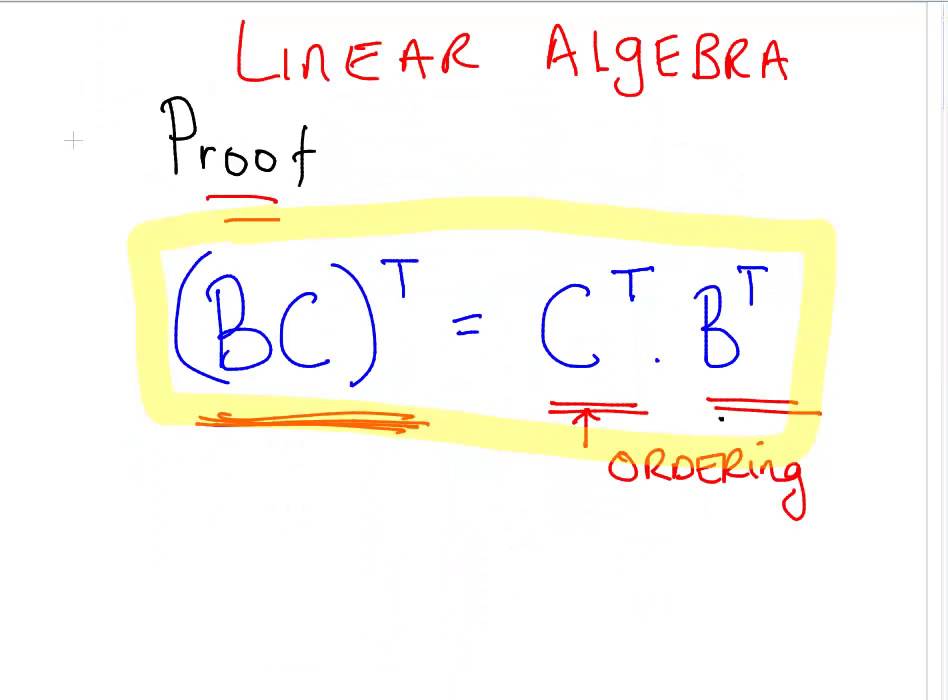
Transpose of a product. Matrix transpose AT 15 33 52 21 A 1352 532 1 Example Transpose operation can be viewed as flipping entries about the diagonal. ABC T C T B T A T.
BnTis an1column matrix then the productABis defined as ABa1a2. Matrix Algebra Theorem 3 Algebraic Properties of Matrix Multiplication 1. So A B is also an m n matrix.
A-B B-A the other rule in subtraction of algebra are also valid in subtraction of matrices Transpose a matrix. DTAx n k 1 n ℓ 1xkdℓaℓ k. Transpose Dot Product Def.
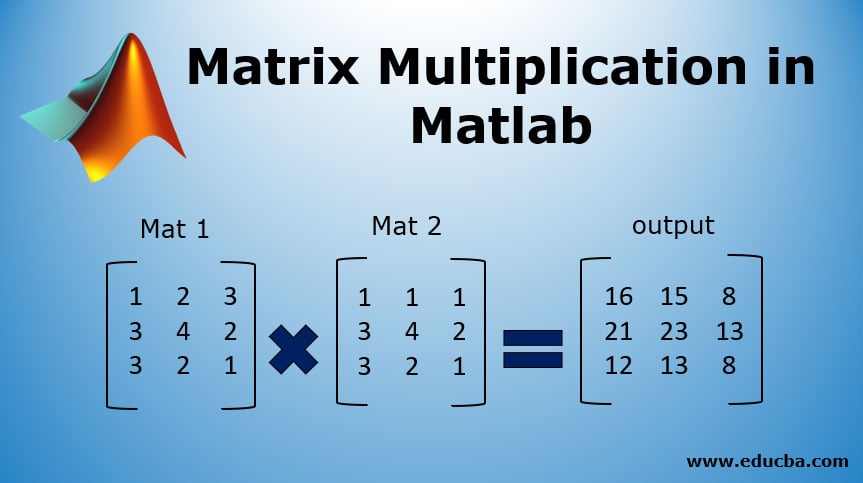
Then we can write ABCT ABCT. That is kA kA where k is a constant. M1 transposecA m2 ctransposeA allallm1 m2 if this equals 1 then the two matrices are equal m1 105000 84000 -168000 0 21000 0 m2 105000 84000 -168000 0 21000 0 ans 1 Rule 4 B 0 2.
If A is symmetric then ai j aj i for all ai j A. If A 1 2 3 4 5 6 then AT 2 4 1 4 2 5 3 6 3 5. AB is just a matrix so we can use the rule we developed for the transpose of the product to two matrices to get ABCT CT ABT CT BT AT.
Also At and Bt are n m matrices. Anis a1nrow matrix andB b1b2. That is the beauty of having properties like associative.
You have to repeat this procedure for every element of C but lets zoom in on that one specific but arbitrary element on position i j for now. So in this case xTAd dTAx. And the transpose of the transpose matrix.
We can multiply a number aka. Rule 3 c 21. Here A and B are two matrices of size m n.
Of taking the transpose is an involution. This property says that A Bt At Bt. So that the Transpose of A B or A Bt is an n m matrix.
The transpose of the product of two matrices is equivalent to the product of their transposes in reversed order. Scalar by a matrix by multiplying every entry of the matrix by the scalar this is denoted by juxtaposition or with the scalar on the left. From now on vectors v 2Rn will be regarded as columns ie.
Let us use the fact that matrix multiplication is associative that is ABCA BC. AB T B T A T The same is true for the product of multiple matrices. The rows of AT are the columns of A.
Recall that ifMis a matrix then the transpose ofM writtenMT is the matrix obtained fromMby writing the rows ofMas thecolumns ofMT. ABC ABCAssociativity of matrix mul-tiplication. Ie AT ij A ji ij.
And then you add these n products. Find the transpose of the matrix and verify that A T T A. Using this fact and switching the sums around in 2 yields dTAx n ℓ 1 n k 1xℓdkak ℓ n ℓ 1 n k 1xℓdkaℓ k.
A is the transpose and A -1 is the inverse of A. The numbers in a row move to be column and vice versa. The columns of AT are the rows of A.
2 1 6 9 3 6 0 2 12 18 6 12 0 sometimes you see scalar multiplication with the scalar on the right α βA αAβA.
Multiplying Matrices Article Matrices Khan Academy

Linear Algebra Learning The First Chapter And The Matrix Equations 1 4 Matrix Algebra Programmer Sought
Linear Algebra Transpose Matrices Proof Youtube
Properties Of Matrix Multiplication Article Khan Academy

7 1 Matrices Vectors Addition And Scalar Multiplication
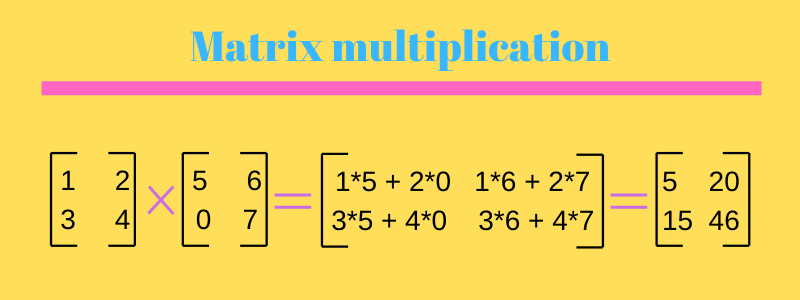
Matrix Multiplication In C Programming Simplified

Matrix Multiplication An Overview Sciencedirect Topics
Matrix Multiplication In Matlab How To Perform Matrix Multiplication

When Writing This Lorentz Transform As A Matrix Why Do We Take The Transpose Physics Stack Exchange

Rules Of Matrix Arithmetic Ppt Video Online Download

7 1 Matrices Vectors Addition And Scalar Multiplication

Chapter 2 Matrices 2 1 Operations With Matrices

Matrix Multiplication With A Transpose Example Youtube
What Does It Mean To Square A Matrix Quora

7 1 Matrices Vectors Addition And Scalar Multiplication

Chapter 2 Matrices 2 1 Operations With Matrices

Rules Of Matrix Arithmetic Ppt Video Online Download